Versão para Impressão

Conceitos básicos de arquitetura de computadores

Robôs modernos são essencialmente sistemas computacionais complexos que interagem com o mundo físico, sendo assim, é muito útil entender os conceitos básicos de arquitetura de computadores.

Primeiramente, é comum distinguir entre arquitetura de computadores e organização de computadores. Embora as definições exatas possam ser difíceis de estabelecer, existe um consenso sobre as áreas que cada termo abrange. ^[1]

• Arquitetura de computador refere-se aos atributos de um sistema que são visíveis a um programador e que têm um impacto direto na execução lógica de um programa. Um termo frequentemente usado de forma intercambiável é arquitetura de conjunto de instruções (ISA), que define os formatos das instruções, códigos de operação (opcodes), registradores, memória de dados e instrução, o efeito das instruções executadas e um algoritmo para o controle da execução.
• Organização de computador refere-se às unidades operacionais e suas interconexões que implementam as especificações da arquitetura. Isso inclui detalhes de hardware transparentes ao programador, como sinais de controle, interfaces com periféricos e a tecnologia de memória utilizada.

Por exemplo, decidir se um computador terá uma instrução de multiplicação é uma questão de arquitetura, enquanto decidir se essa instrução será implementada por uma unidade de multiplicação dedicada ou usando repetidamente a unidade de adição é uma questão de organização. Muitos fabricantes oferecem famílias de computadores com a mesma arquitetura, mas com diferentes organizações, resultando em diferentes características de preço e desempenho.

Um sistema de computador, como qualquer sistema, consiste em um conjunto inter-relacionado de componentes. Ele pode ser caracterizado em termos de estrutura (a forma como os componentes estão interligados) e função (a operação dos componentes individuais). Ao estudar o hardware de um computador digital, é essencial observar tanto a sua estrutura quanto a sua função. A estrutura define como os componentes se inter-relacionam, enquanto a função define a funcionalidade específica de cada componente.

Um computador: estrutura de alto nível

Em termos gerais, existem quatro funções básicas que um computador pode realizar:

• Processamento de dados: Os dados podem ter diversas formas, e o processamento pode variar amplamente, mas existem métodos e tipos fundamentais de processamento.

• Armazenamento de dados: O computador precisa armazenar dados temporariamente para processamento imediato e também a longo prazo para recuperação e atualização.

• Movimentação de dados: O computador deve ser capaz de transferir dados entre seus componentes e com o mundo exterior (entrada e saída).

• Controle: Uma unidade de controle dentro do computador gerencia os recursos e coordena o desempenho das partes funcionais em resposta às instruções.

Do ponto de vista da estrutura, um computador digital é composto por vários componentes principais:

• Unidade Central de Processamento (CPU): Controla a operação do computador e realiza suas funções de processamento de dados. A CPU geralmente é referida como o processador. Ela inclui a Unidade de Controle, que controla a operação da CPU e do computador, e a Unidade Lógica e Aritmética (ALU), que executa as funções de processamento de dados. A CPU também contém registradores para armazenamento interno.
• Memória: Armazena dados e instruções.
• Periféricos (Entrada e Saída): Permitem a comunicação com o mundo exterior. Dispositivos de entrada enviam informações para outros componentes, e dispositivos de saída recebem informações. Um controlador é responsável por controlar um dispositivo de E/S e seu acesso ao barramento.
• Barramentos: São conjuntos de condutores que proporcionam comunicação entre a CPU, memória e periféricos. O projeto da estrutura de interconexão, incluindo o uso de barramentos, é crucial.

A maioria dos computadores modernos é baseada na arquitetura de Von-Neumann, que possui três conceitos principais:

• Dados e instruções são armazenados em uma única memória de leitura e escrita.
• O conteúdo dessa memória é endereçável pela localização, independentemente do tipo de dado armazenado.
• A execução das instruções ocorre de forma sequencial (a menos que explicitamente modificada).

A função básica de um computador é executar programas armazenados na memória. Isso envolve um ciclo de busca e execução de instruções. A unidade de controle busca as instruções na memória, determina seu tipo e a unidade de lógica e aritmética (ULA) efetua as operações necessárias. ^[2]

Existem diferentes abordagens para o projeto de arquitetura de computadores, como CISC (Complex Instruction Set Computers) e RISC (Reduced Instruction Set Computers). A arquitetura x86 é um exemplo de CISC, enquanto a arquitetura ARM é um exemplo de RISC.

• CISC historicamente visava simplificar os compiladores e melhorar o desempenho através de instruções mais complexas.
• RISC surgiu como uma alternativa, enfatizando um conjunto de instruções simples e limitado, um grande número de registradores e a otimização do pipeline de instruções.

Conceitos como paralelismo também são importantes em arquitetura de computadores para melhorar o desempenho. Isso pode envolver a execução de múltiplas instruções simultaneamente (paralelismo no nível da instrução) ou o uso de múltiplos processadores (paralelismo no nível do processador ou computadores multicore).

Entender esses conceitos fundamentais ajudará na compreensão de como os sistemas robóticos processam informações, controlam seus atuadores e interagem com sensores, que são todos aspectos cruciais da robótica.

PCs (Personal Computers):

• PCs são sistemas de computação de propósito geral encontrados em desktops, laptops e servidores.
• Eles geralmente utilizam a arquitetura Intel x86 ou, no caso de alguns laptops e tablets (como o iPad), podem usar outras arquiteturas, como ARM.
• Os PCs são projetados para uma ampla gama de tarefas, desde navegação na internet e processamento de texto até jogos, desenvolvimento de software e operação de servidores.
• Eles possuem unidades de processamento central (CPUs) poderosas com recursos como múltiplos núcleos (multicore) e caches de memória.
• PCs têm sistemas operacionais complexos, como Windows e Linux, que gerenciam recursos de hardware e software.
• Eles oferecem ampla capacidade de memória (RAM e armazenamento secundário, como HDDs ou SSDs).
• PCs suportam uma grande variedade de periféricos e interfaces de E/S (Entrada/Saída), como USB e PCIe.

Arduino:

• Arduino é uma plataforma de prototipagem eletrônica de código aberto baseada em microcontroladores AVR.
• É projetado para ser simples e acessível para artistas, designers, hobistas e qualquer pessoa interessada em criar projetos interativos ou ambientes.
• Os Arduinos geralmente possuem poder de processamento limitado em comparação com PCs, com CPUs de 8 bits em muitos modelos.
• Eles têm quantidades menores de memória (SRAM e Flash).
• A programação do Arduino é feita tipicamente em C/C++ usando a IDE (Integrated Development Environment) do Arduino, que simplifica o processo de desenvolvimento para interagir com o hardware.
• Arduinos são ideais para controlar dispositivos eletrônicos, ler sensores e interagir com o mundo físico através de pinos de E/S.
• São frequentemente usados em sistemas embarcados de menor complexidade.
• O custo de um Arduino é geralmente muito menor do que o de um PC.

ESP (Exemplo: ESP32 ou ESP8266):

• ESP se refere comumente a microcontroladores como o ESP32 e ESP8266, que são populares para projetos de Internet das Coisas (IoT).
• Esses microcontroladores geralmente possuem mais poder de processamento e memória do que muitos modelos de Arduino, com CPUs de 32 bits e recursos como Wi-Fi integrado.
• A arquitetura subjacente é tipicamente ARM, que é usada em sistemas embarcados e dispositivos móveis.
• Assim como o Arduino, os ESPs são usados para controlar periféricos, interagir com sensores e atuadores, mas com um foco maior em conectividade de rede devido ao Wi-Fi integrado.
• São amplamente utilizados em sistemas embarcados e aplicações de IoT onde a comunicação sem fio é essencial.
• O custo dos ESPs geralmente se situa entre o de um Arduino básico e um PC, sendo mais acessíveis que os PCs.

Comparativo Resumido:

A tabela a seguir resume algumas das principais diferenças:

Característica	PC (Ex: x86 Laptop)	Arduino (Ex: Uno)	ESP (Ex: ESP32)
Arquitetura Típica	Intel x86 ou ARM	AVR	ARM
Poder de Processamento	Alto	Baixo	Médio
Memória	Grande	Pequena	Média
Sistema Operacional	Complexo (Windows, Linux, macOS)	Nenhum	Nenhum
Conectividade de Rede	Ethernet, Wi-Fi (geralmente)	Requer módulos adicionais	Wi-Fi integrado (na maioria)
Foco Principal	Propósito geral	Controle eletrônico, prototipagem	IoT, controle com conectividade
Custo	Alto	Muito baixo	Baixo a médio
Complexidade	Alta	Baixa	Média

Ilustração Conceitual:

Imagine um espectro de sistemas de computação.

• Em uma extremidade, temos o PC, que é como um canivete suíço de alta potência – capaz de fazer muitas coisas complexas, com muitos recursos, mas também mais caro e complexo de operar para tarefas simples. Visualmente, pense em um laptop moderno com uma tela grande e muitos botões e portas.

• No meio, podemos colocar o ESP, que seria como uma ferramenta multifuncional especializada em comunicação – ainda capaz de controlar coisas, mas com um foco forte em se conectar a redes sem fio e à internet. Imagine uma pequena placa com um chip proeminente e uma antena.

• Na outra extremidade, está o Arduino, que é como uma chave de fenda – simples, direta e muito boa para tarefas específicas de controle eletrônico. Visualmente, pense em uma placa com poucos componentes grandes e pinos facilmente acessíveis para conectar fios.

PCs (Computadores Pessoais):

• Arquitetura de Computadores: A arquitetura de PCs é tipicamente baseada em x86 (predominantemente CISC, embora com influências RISC em implementações modernas). Em alguns laptops e tablets, também se encontra a arquitetura ARM (RISC). A arquitetura define o conjunto de instruções, os tipos de dados, os mecanismos de entrada/saída (E/S) e as técnicas de endereçamento de memória visíveis ao programador. A arquitetura x86, historicamente, evoluiu para oferecer um conjunto de instruções complexo (CISC), enquanto a ARM é essencialmente uma arquitetura de conjunto de instruções reduzido (RISC).
• Organização de Computadores: A organização de PCs geralmente segue a arquitetura de Von Neumann, onde a unidade central de processamento (CPU), a memória e os componentes de E/S são interconectados. A CPU contém a unidade de controle, a unidade lógica e aritmética (ULA) e registradores. PCs possuem uma hierarquia de memória complexa, incluindo múltiplos níveis de cache, memória principal (RAM) e armazenamento secundário. A interconexão entre os componentes é realizada por barramentos de alta velocidade, como o PCI Express (PCIe) e Universal Serial Bus (USB). Os PCs modernos frequentemente utilizam processadores multicore, com múltiplos núcleos de processamento no mesmo chip.

Arduino:

• Arquitetura de Computadores: O Arduino é baseado principalmente em microcontroladores da família AVR. A arquitetura AVR é mais simples em comparação com x86 ou ARM, com um conjunto de instruções menor e modos de endereçamento mais diretos.
• Organização de Computadores: A organização do Arduino é centrada em um único microcontrolador. Este chip integra a CPU (tipicamente de 8 bits), memória (SRAM e Flash de capacidade limitada) e diversos periféricos (pinos de E/S digital e analógica, comunicação serial, etc.). A interconexão dos componentes é interna ao chip do microcontrolador, sendo mais direta e menos complexa que a de um PC. A principal forma de interação com o mundo externo é através dos pinos de E/S. A organização é otimizada para controle em tempo real de dispositivos eletrônicos e prototipagem, com foco na simplicidade e baixo custo.

ESP32/ESP8266:

• Arquitetura de Computadores: Os microcontroladores ESP32 e ESP8266 são baseados na arquitetura ARM. A ARM é uma arquitetura RISC, oferecendo um equilíbrio entre desempenho e eficiência energética, sendo amplamente utilizada em sistemas embarcados e dispositivos móveis. A arquitetura ARM define um conjunto de instruções mais eficiente para certas tarefas em comparação com CISC.
• Organização de Computadores: A organização dos ESPs é mais complexa que a do Arduino, mas ainda mais integrada que a de um PC. Eles incorporam um processador ARM de 32 bits, uma quantidade maior de memória (SRAM e Flash) em comparação com o Arduino, e recursos de conectividade de rede integrados, como Wi-Fi e Bluetooth (no caso do ESP32). Além dos pinos de E/S, eles possuem controladores para comunicação sem fio, tornando-os ideais para aplicações de Internet das Coisas (IoT). A interconexão dos componentes é feita internamente no chip, utilizando barramentos para a comunicação entre a CPU, memória e periféricos. A organização visa um bom desempenho em tarefas de processamento e comunicação com baixo consumo de energia.

Em resumo:

• Os PCs possuem arquiteturas (x86 ou ARM) e organizações complexas, projetadas para alto desempenho e versatilidade em uma ampla gama de aplicações.
• O Arduino utiliza uma arquitetura (AVR) e organização mais simples, focadas no controle eletrônico direto, baixo custo e facilidade de uso para prototipagem.
• Os ESPs empregam a arquitetura ARM e uma organização intermediária, oferecendo um bom equilíbrio entre poder de processamento, conectividade de rede integrada e baixo consumo de energia, sendo ideais para aplicações de IoT e sistemas embarcados conectados.

A distinção entre arquitetura e organização é crucial para entender as capacidades e limitações de cada um desses sistemas. A arquitetura dita o que o sistema pode fazer do ponto de vista do software, enquanto a organização determina como essas funcionalidades são implementadas no hardware.

Referências

Sistemas de Numeração e Sistema Binário

Introdução aos Sistemas de Numeração

Os sistemas de numeração são métodos utilizados para representar quantidades através de símbolos. Ao longo da história, diferentes civilizações desenvolveram seus próprios sistemas para representar números, cada um com características específicas que refletem as necessidades e o contexto cultural de cada época.

No mundo da computação e dos sistemas digitais, compreender diferentes sistemas de numeração é fundamental, pois os computadores não processam informações da mesma forma que nós, humanos. Enquanto estamos acostumados a utilizar o sistema decimal (base 10) em nosso dia a dia, os computadores operam fundamentalmente com o sistema binário (base 2).

Sistemas de Numeração Posicional

Os sistemas de numeração que utilizamos atualmente são chamados de sistemas posicionais. Isso significa que o valor de um dígito depende não apenas do símbolo utilizado, mas também da posição que ele ocupa no número. Por exemplo, no número decimal 123, o dígito "1" representa uma centena (10²), o "2" representa duas dezenas (10¹) e o "3" representa três unidades (10⁰).

Características de um Sistema de Numeração Posicional:

1. Base: Número de símbolos distintos utilizados no sistema.
2. Símbolos: Conjunto de caracteres utilizados para representar quantidades.
3. Valor posicional: O valor de um dígito depende da sua posição no número.
4. Peso: Cada posição tem um peso associado, que é uma potência da base.

Principais Sistemas de Numeração

Sistema de numerção e suas Bases

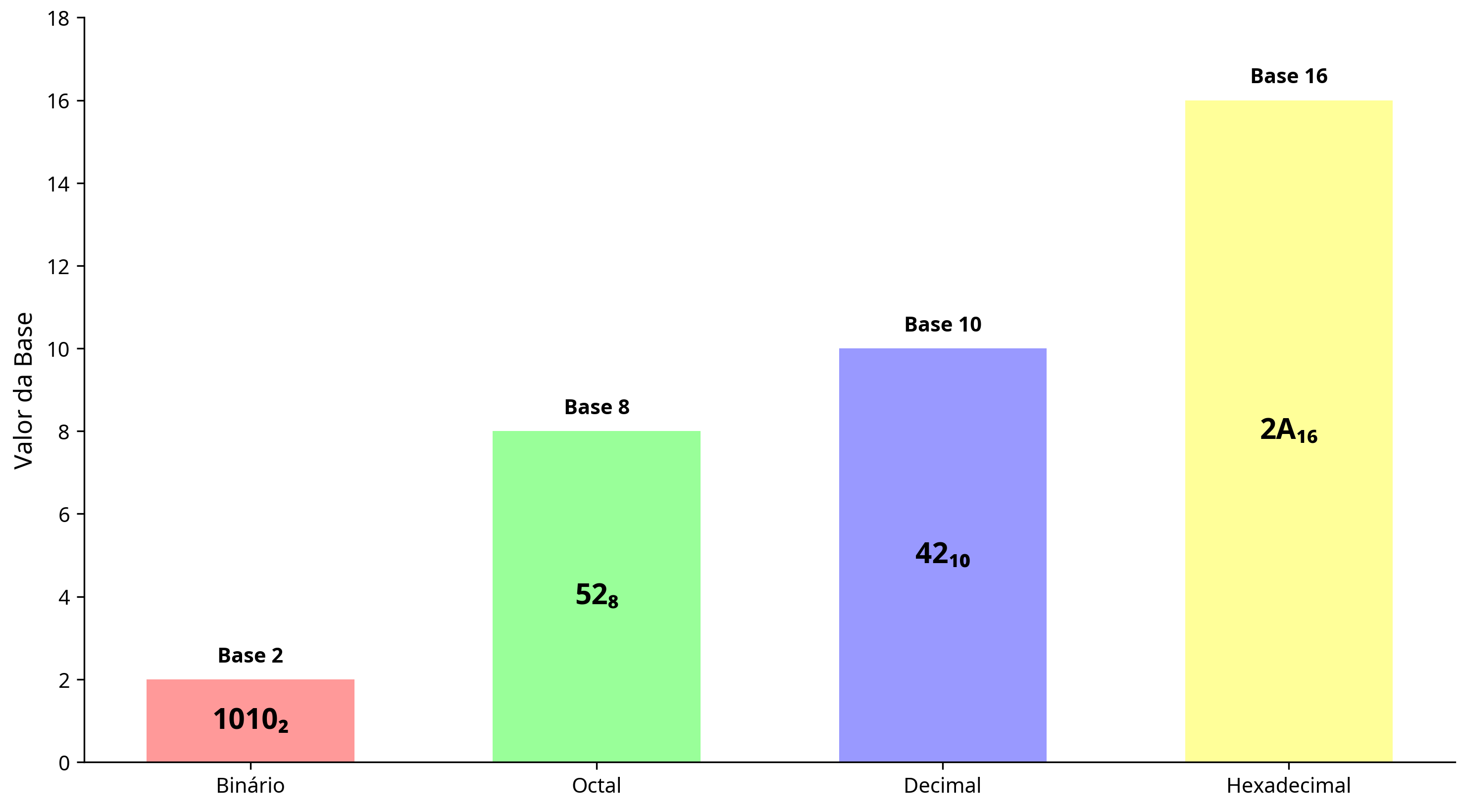
Sistema Decimal (Base 10)

Sistema Decimal (Base 10)

Símbolos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Exemplo: 18724

O sistema decimal é o mais familiar para nós, pois é o que utilizamos no cotidiano. Ele utiliza 10 símbolos distintos: 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9.

Exemplo: O número decimal 425 pode ser interpretado como:

• 4 × 10² = 4 × 100 = 400
• 2 × 10¹ = 2 × 10 = 20
• 5 × 10⁰ = 5 × 1 = 5
• Total: 400 + 20 + 5 = 425

Sistema Binário (Base 2)

O sistema binário utiliza apenas dois símbolos: 0 e 1. É o sistema fundamental para a computação, pois os circuitos eletrônicos podem facilmente representar dois estados: ligado (1) ou desligado (0).

Sistema Binário (Base 2)

Símbolos: 0, 1

Exemplo: 10101₂

Exemplo: O número binário 1011₂ pode ser interpretado como:

• 1 × 2³ = 1 × 8 = 8
• 0 × 2² = 0 × 4 = 0
• 1 × 2¹ = 1 × 2 = 2
• 1 × 2⁰ = 1 × 1 = 1
• Total: 8 + 0 + 2 + 1 = 11 (em decimal)

Outro exemplo

Represetnação Binária do Número 10110101

Sistema Octal (Base 8)

O sistema octal utiliza 8 símbolos: 0, 1, 2, 3, 4, 5, 6 e 7.

Sistema Octal (Base 8)

Símbolos: 0, 1, 2, 3, 4, 5, 6, 7
Exemplo: 7634₈

Exemplo: O número octal 347₈ pode ser interpretado como:

• 3 × 8² = 3 × 64 = 192
• 4 × 8¹ = 4 × 8 = 32
• 7 × 8⁰ = 7 × 1 = 7
• Total: 192 + 32 + 7 = 231 (em decimal)

Sistema Hexadecimal (Base 16)

O sistema hexadecimal utiliza 16 símbolos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E e F, onde A representa 10, B representa 11, e assim por diante até F, que representa 15.

Sistema Hexadecimal (Base 16)

Símbolos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Exemplo: AB43₁₆

Exemplo: O número hexadecimal 2AF pode ser interpretado como:

• 2 × 16² = 2 × 256 = 512
• A (10 em decimal) × 16¹ = 10 × 16 = 160
• F (15 em decimal) × 16⁰ = 15 × 1 = 15
• Total: 512 + 160 + 15 = 687 (em decimal)

Conversão Entre Sistemas de Numeração

Conversor Numérico: Decimal ↔ Binário ↔ Octal ↔ Hexadecimal

Decimal:

Binário:

Octal:

Hexadecimal:

Conversão de Decimal para Outra Base

Para converter um número decimal para outra base, dividimos sucessivamente o número pela base desejada, anotando os restos das divisões. O número na nova base é formado pelos restos lidos de baixo para cima.

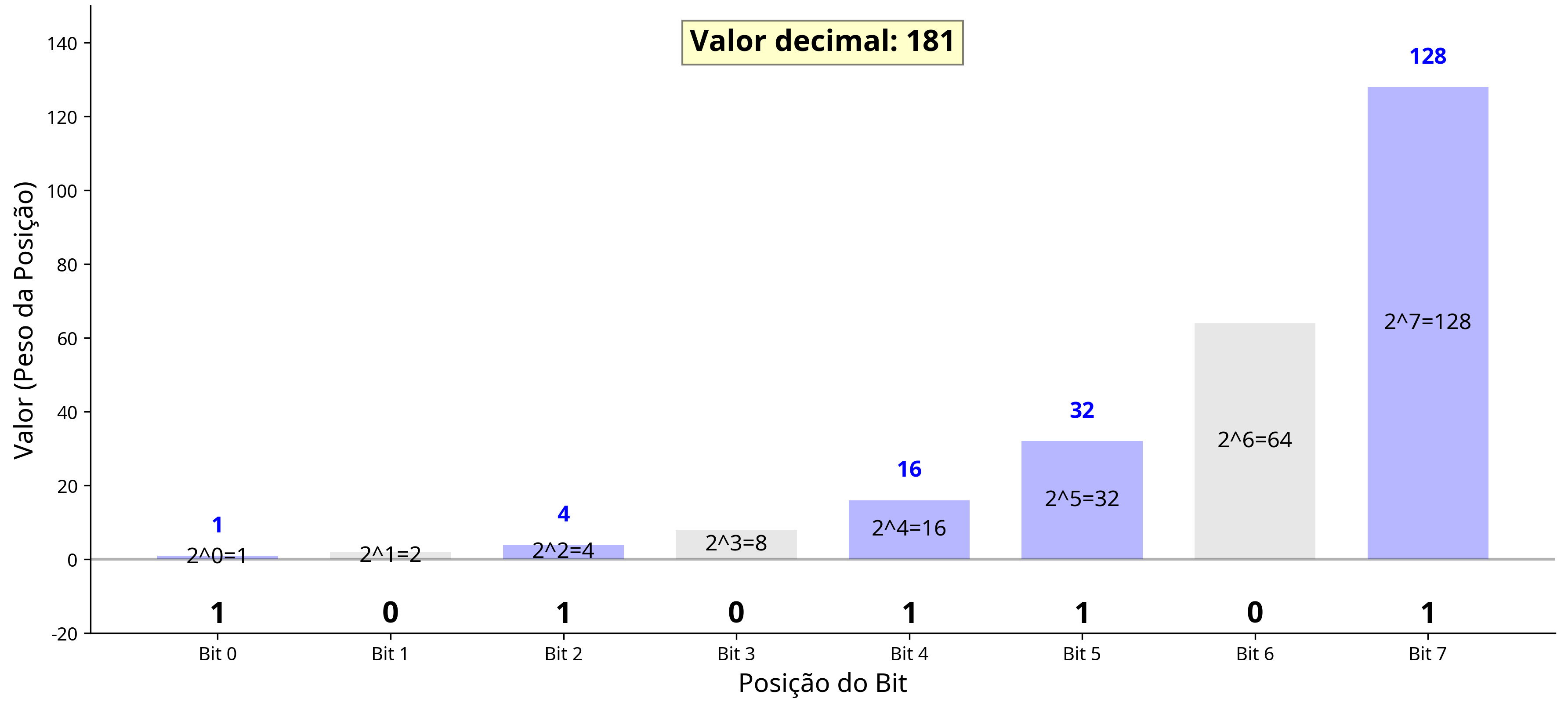
Exemplo: Conversão de 42 (decimal) para binário:

• 42 ÷ 2 = 21, resto 0
• 21 ÷ 2 = 10, resto 1
• 10 ÷ 2 = 5, resto 0
• 5 ÷ 2 = 2, resto 1
• 2 ÷ 2 = 1, resto 0
• 1 ÷ 2 = 0, resto 1
• Resultado: 101010 (binário)

Conversão de Outra Base para Decimal

Para converter um número de qualquer base para decimal, multiplicamos cada dígito pelo valor da base elevado à potência correspondente à posição do dígito, e somamos todos os resultados.

Exemplo: Conversão de 1101 (binário) para decimal:

• 1 × 2³ = 1 × 8 = 8
• 1 × 2² = 1 × 4 = 4
• 0 × 2¹ = 0 × 2 = 0
• 1 × 2⁰ = 1 × 1 = 1
• Total: 8 + 4 + 0 + 1 = 13 (decimal)

Conversão Direta Entre Bases Não Decimais

Para converter entre bases não decimais (por exemplo, de binário para hexadecimal), geralmente é mais fácil usar o decimal como intermediário. No entanto, existem alguns atalhos úteis:

Binário para Octal

Agrupe os dígitos binários em grupos de 3, da direita para a esquerda, e converta cada grupo para o dígito octal correspondente.

Exemplo:

Vamos converter o número binário 1011011₂ para octal:

Agrupando em grupos de 3 (da direita para a esquerda): 10 | 110 | 011
Completando com zeros à esquerda no primeiro grupo: 010 | 110 | 011
Convertendo cada grupo para octal:
010 = 2 (em octal)
110 = 6 (em octal)
011 = 3 (em octal)

Resultado: 263₈ (octal)

Binário para Hexadecimal

Agrupe os dígitos binários em grupos de 4, da direita para a esquerda, e converta cada grupo para o dígito hexadecimal correspondente.

Exemplo:

Conversão de 1011010 (binário) para hexadecimal:

• Agrupando em grupos de 4: 101 1010
• Completando com zeros à esquerda: 0101 1010
• Convertendo cada grupo: 0101 = 5, 1010 = A
• Resultado: 5A₁₆ (hexadecimal)

O Sistema Binário em Detalhes

O sistema binário é a base de toda a computação moderna. Vamos explorar mais a fundo suas características e aplicações.

Por que o Sistema Binário é Usado em Computadores?

1. Simplicidade: Com apenas dois estados (0 e 1), é fácil representar informações usando componentes eletrônicos que podem estar em um de dois estados (ligado/desligado).
2. Confiabilidade: A distinção entre dois estados é mais robusta contra ruídos e interferências do que sistemas com mais estados.
3. Facilidade de implementação: Circuitos digitais que operam com dois estados são mais simples de projetar e fabricar.

Representação de Informações em Binário

Bit e Byte

• Bit: A menor unidade de informação em um sistema digital, que pode assumir apenas um de dois valores: 0 ou 1.
• Byte: Um conjunto de 8 bits, capaz de representar 2⁸ = 256 valores diferentes (de 0 a 255).

Operações Aritméticas em Binário

Adição Binária

A adição binária segue regras simples:

• 0 + 0 = 0
• 0 + 1 = 1
• 1 + 0 = 1
• 1 + 1 = 10 (0 com carry 1)

Exemplo:

  1 1 1 (carry)
  1 0 1 1
+ 0 1 0 1
---------
1 0 0 0 0

Subtração Binária

A subtração binária pode ser realizada diretamente ou utilizando o complemento de 2:

• 0 - 0 = 0
• 1 - 0 = 1
• 1 - 1 = 0
• 0 - 1 = 1 (com borrow 1)

Exemplo usando complemento de 2:
Para calcular 7 - 3:

• 7 em binário: 0111
• 3 em binário: 0011
• Complemento de 2 de 3: 1101
• 0111 + 1101 = 0100 (ignorando o carry)
• Resultado: 0100 = 4 em decimal

Aplicações do Sistema Binário

Codificação de Caracteres

Os caracteres de texto são representados em computadores através de códigos binários. Alguns padrões comuns incluem:

• ASCII: Utiliza 7 bits para representar 128 caracteres diferentes, incluindo letras, números e símbolos.
• Unicode: Estende o ASCII para incluir caracteres de praticamente todos os sistemas de escrita do mundo, utilizando mais bits por caractere.

Representação de Imagens

As imagens digitais são compostas por pixels, cada um representado por um conjunto de bits que definem sua cor. Por exemplo:

• Imagem em preto e branco: Cada pixel pode ser representado por 1 bit (0 para preto, 1 para branco).
• Escala de cinza: Cada pixel pode ser representado por vários bits para indicar diferentes níveis de cinza.
• Imagem colorida: Cada pixel é representado por bits que definem as intensidades de vermelho, verde e azul (RGB).

Representação de Áudio

O áudio digital é representado através da amostragem do sinal sonoro em intervalos regulares, com cada amostra sendo convertida em um valor binário.

Conclusão

Os sistemas de numeração, especialmente o sistema binário, são fundamentais para a computação e os sistemas digitais. Compreender como esses sistemas funcionam e como realizar conversões entre eles é essencial para qualquer pessoa que deseje trabalhar com tecnologia digital.

Na próxima aula, exploraremos as funções e portas lógicas, que são os blocos básicos de construção dos circuitos digitais, e veremos como eles utilizam o sistema binário para realizar operações lógicas.

Exercícios Propostos

1. Converta os seguintes números decimais para binário:
   a) 25
   b) 42
   c) 127
   d) 255

2. Converta os seguintes números binários para decimal:
   a) 1010
   b) 11011
   c) 10101010
   d) 11111111

3. Realize as seguintes operações em binário:
   a) 1011 + 1101
   b) 10110 - 1101

4. Converta os seguintes números:
   a) 42 (decimal) para hexadecimal
   b) A7 (hexadecimal) para decimal
   c) 1101 0111 (binário) para octal
   d) 753 (octal) para binário

Link para entrega

icon: pen-to-square
date: 2025-04-15 10:20:00.00 -3
category:

• aula
• exercicio
• entrega
  order: 3

---

Álgebra Booleana e Circuitos Lógicos

Uma álgebra Booleana pode ser definida com um conjunto de operadores e um conjunto de axiomas, que são assumidos verdadeiros sem necessidade de prova.

Em 1854, George Boole introduziu o formalismo que até hoje se usa para o tratamento sistemático da lógica, que é a chamada Álgebra Booleana. Em 1938, C. E. Shannon aplicou esta álgebra para mostrar que as propriedades de circuitos elétricos de chaveamento podem ser representadas por uma álgebra Booleana com dois valores.

Diferentemente da álgebra ordinária dos reais, onde as variáveis podem assumir valores no intervalo (-∞;+∞), as variáveis Booleanas só podem assumir um número finito de valores. Em particular, na álgebra Booleana de dois valores, cada variável pode assumir um dentre dois valores possíveis, os quais podem ser denotados por [F,V] (falso ou verdadeiro), [H,L] (high and low) ou ainda [0,1]. Mais para frente, adotaremos apenas a notação [0,1], a qual também é utilizada em eletrônica digital.

Como o número de valores que cada variável pode assumir é finito (e pequeno), o número de estados que uma função Booleana pode assumir também será finito, o que significa que podemos descrever completamente as funções Booleanas utilizando tabelas. Devido a este fato, uma tabela que descreva uma função Booleana recebe o nome de tabela verdade, e nela são listadas todas as combinações de valores que as variáveis de entrada podem assumir e os correspondentes valores da função (saídas).

Operações Básicas da Álgebra Booleana (ou Álgebra de Chaveamento)

Na álgebra Booleana, existem três operações ou funções básicas: operação OU, operação E e complementação. Todas as funções Booleanas podem ser representadas em termos destas operações básicas.

Operação OU (Adição Lógica)

Uma definição para a operação OU, que também é denominada adição lógica, é:

Info

A operação OU resulta 1 se pelo menos uma das variáveis de entrada vale 1.

Como uma variável Booleana ou vale 1 ou vale 0, e como o resultado de uma operação qualquer pode ser encarado como (ou atribuído a) uma variável Booleana, basta que definamos quando a operação vale 1. Automaticamente, a operação resultará 0 nos demais casos. Assim, pode-se dizer que a operação OU resulta 0 somente quando todas as variáveis de entrada valem 0.

Um símbolo possível para representar a operação OU é “+”, tal como o símbolo da adição algébrica (dos reais). Porém, como estamos trabalhando com variáveis Booleanas, sabemos que não se trata da adição algébrica, mas sim da adição lógica. Outro símbolo também encontrado na bibliografia é “Ú”.

Listando as possibilidades de combinações entre dois valores Booleanos e os respectivos resultados para a operação OU, tem-se:

 0 + 0 = 0 
 0 + 1 = 1 
 1 + 0 = 1 
 1 + 1 = 1

Note que a operação OU só pode ser definida se houver, pelo menos, duas variáveis envolvidas. Ou seja, não é possível realizar a operação sobre somente uma variável. Devido a isso, o operador “+” (OU) é dito binário.

Nas equações, não costuma-se escrever todas as possibilidades de valores. Apenas adotamos uma letra (ou uma letra com um índice) para designar uma variável Booleana. Com isso, já se sabe que aquela variável pode assumir ou o valor 0 ou o valor 1. Então, supondo que queiramos demonstrar o comportamento da equação A+B (lê-se A ou B), poderíamos fazê-lo utilizando uma tabela verdade, como segue:

Tabela verdade OU

A	B	A+B
0	0	0
0	1	1
1	0	1
1	1	1

Da mesma forma, podemos mostrar o comportamento da equação A+B+C (lê-se A ou B ou C) por meio de uma tabela verdade. Como na equação há somente o símbolo “+”, trata-se da operação OU sobre três variáveis. Logo, pode-se aplicar diretamente a definição da operação OU: o resultado será 1 se pelo menos uma das variáveis de entrada valer 1.

Tabela verdade A+B+C

A	B	C	A+B+C
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	1

É importante notar que, devido ao fato de haver somente um operador na equação, pode-se também avaliar a equação decompondo-a em pares. Por exemplo, pode-se primeiramente achar o resultado de A+B, para depois operar os valores resultantes com os respectivos valores de C. Esta propriedade é conhecida como associativa. Também a ordem em que são avaliadas as variáveis A, B e C é irrelevante (propriedade comutativa). Estas propriedades são ilustradas pela tabela verdade a seguir. Nela, os parênteses indicam subexpressões já avaliadas em coluna imediatamente à esquerda. Note que os valores das colunas referentes às expressões A+B+C, (A+B)+C e (B+C)+A são os mesmos (na mesma ordem).

Propriedade associativa e comutativa do OU

A	B	C	A+B+C	A+B	(A+B)+C	B+C	(B+C)+A
0	0	0	0	0	0	0	0
0	0	1	1	0	1	1	1
0	1	0	1	1	1	1	1
0	1	1	1	1	1	1	1
1	0	0	1	1	1	0	1
1	0	1	1	1	1	1	1
1	1	0	1	1	1	1	1
1	1	1	1	1	1	1	1

Operação E (Multiplicação Lógica)

A operação E, ou multiplicação lógica, pode ser definida da seguinte forma:

Info

A operação E resulta 0 se pelo menos uma das variáveis de entrada vale 0

Pela definição dada, pode-se deduzir que o resultado da operação E será 1 se, e

somente se, todas as entradas valerem 1.

O símbolo usualmente utilizado na operação E é “×”, porém outra notação possível é “Ù”. Podemos, também, listar as possibilidades de combinações entre dois valores Booleanos e os respectivos resultados, para a operação E:

0 × 0    =     0 
0 × 1    =     0 
1 × 0    =     0 
1 × 1    =     1

Assim como a operação OU, a operação E só pode ser definida entre, pelo menos duas variáveis. Ou seja, o operador “×” (E) também é binário.
Para mostrar o comportamento da equação A × B (lê-se A e B), escreve-se uma tabela

Tabela verdade E

A	B	A×B
0	0	0
0	1	0
1	0	0
1	1	1

De forma semelhante, pode-se determinar o resultado da equação A×B×C (lê-se A e B e C) utilizando diretamente a definição da operação E: o resultado será 0 se pelo menos uma das variáveis de entrada valer 0.

Tabela verdade AxBxC

A	B	C	A×B×C
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	0
1	0	0	0
1	0	1	0
1	1	0	0
1	1	1	1

Também para a operação E valem as propriedades associativa e comutativa. Então, a equação A×BC pode ainda ser avaliada tomando-se as variáveis aos pares, em qualquer ordem.

Veja a tabela verdade a seguir e compare os resultados.

Propriedade associativa e comutativa do OU

A	B	C	A×B×C	A×B	(A×B)×C	B×C	A×(B×C)
0	0	0	0	0	0	0	0
0	0	1	0	0	0	0	0
0	1	0	0	0	0	0	0
0	1	1	0	0	0	1	0
1	0	0	0	0	0	0	0
1	0	1	0	0	0	0	0
1	1	0	0	1	0	0	0
1	1	1	1	1	1	1	1

Complementação (ou Negação, ou Inversão)

A operação 'complementação dispensa uma definição. É a operação cujo resultado é simplesmente o valor complementar ao que a variável apresenta. Também devido ao fato de uma variável Booleana poder assumir um entre somente dois valores, o valor complementar será 1 se a variável vale 0 e será 0 se a variável vale 1.

Os símbolos utilizados para representar a operação complementação sobre uma variável Booleana A são $\bar{A}$ , ~A e A' (lê-se A negado). Nesta disciplina, adotaremos o primeiro símbolo. O resultado da operação complementação pode ser listado:

$\bar{0}=1$

$\bar{1}=0$

Diferentemente das operações OU e E, a complementação só é definida sobre uma variável, ou sobre o resultado de uma expressão. Ou seja, o operador complementação é dito unário.

E a tabela verdade para $\bar{A}$ é:

Tabela verdade Negação

A	¬A
0	1
1	0

Avaliação de Expressões Booleanas

Dada a equação que descreve uma função Booleana qualquer, deseja-se saber detalhadamente como esta função se comporta para qualquer combinação das variáveis de entrada. O comportamento de uma função é descrito pela sua tabela verdade e este problema é conhecido como avaliação da função ou da expressão que descreve a função considerada. Em suma, deseja-se achar a tabela verdade para a função Booleana.

Uma tabela verdade consiste basicamente de um conjunto de colunas, nas quais são listadas todas as combinações possíveis entre as variáveis de entrada (à esquerda) e o resultado da função (à direita). Também, pode-se criar colunas intermediárias, onde são listados os resultados de subexpressões contidas na expressão principal. Isto normalmente facilita a avaliação, principalmente no caso de equações muito complexas e/ou contendo muitas variáveis.

Quando numa mesma equação Booleana aparecem operações E e OU, é necessário seguir a ordem de precedência. Tal como na álgebra dos reais, a multiplicação (lógica) tem precedência sobre a adição (lógica). Além disso, expressões entre parêntesis têm precedência sobre operadores E e OU que estejam no mesmo nível. Quanto à complementação, esta deve ser avaliada tão logo seja possível. Caso a complementação seja aplicada sobre uma subexpressão inteira, é necessário que se avalie primeiramente a subexpressão para, só após, inverter o seu resultado.

O número de combinações que as variáveis de entrada podem assumir pode ser calculado por 2ⁿ, onde n é o número de variáveis de entrada.

O procedimento para a criação da tabela verdade a partir de uma equação Booleana é:

1. Criar colunas para as variáveis de entrada e listar todas as combinações possíveis, utilizando a fórmula de combinações = 2ⁿ (onde n é o número de variáveis de entrada);
2. Criar uma coluna para cada variável de entrada que apareça complementada na equação e anotar os valores resultantes;
3. Avaliar a equação seguindo a ordem de precedência, a partir do nível de parêntesis mais internos:
   • Multiplicação lógica
   • Adição lógica

Tomemos como exemplo a expressão $W=X+Y\cdot \bar{Z}$. A variável $W$ representa a função Booleana propriamente dita. Esta variável depende das variáveis que estão à direita do sinal $=$, ou seja, depende de $X$, $Y$ e $Z$. Logo, são 3 as variáveis de entrada. O total de combinações entre 3 variáveis será $2^3=8$. Então, a tabela verdade para $W$ deverá ter 3 colunas à esquerda e 8 linhas. Seguindo o procedimento dado acima, cria-se uma coluna, na qual listam-se os valores para $\bar{Z}$. Após, inicia-se a avaliação propriamente dita, a partir do nível mais interno de parêntesis. Como não há parêntesis na expressão, resolvem-se as subexpressões que envolvem a operação E. No caso em questão, há somente uma tal subexpressão, que é $Y\cdot \bar{Z}$. Então, cria-se uma coluna para $Y\cdot \bar{Z}$, na qual anotam-se os resultados para este produto. Finalmente, utilizam-se os resultados de $Y\cdot \bar{Z}$, listados na coluna anterior, para operar o OU com a variável $X$. Repare os passos descritos na tabela verdade que segue. Nela, os parêntesis em torno do produto $Y\cdot \bar{Z}$ indicam somente que este termo já foi avaliado e que no passo referente a esta coluna, tomaram-se apenas os valores previamente encontrados.

Para a expressão $W=X+Y\cdot \bar{Z}$, a tabela verdade é:

Tabela verdade da expressão W = X + Y × Z

$X$	$Y$	$Z$	$\bar{Z}$	$Y\cdot \bar{Z}$	$W=X+(Y\cdot \bar{Z})$
0	0	0	1	0	0
0	0	1	0	0	0
0	1	0	1	1	1
0	1	1	0	0	0
1	0	0	1	0	1
1	0	1	0	0	1
1	1	0	1	0	1
1	1	1	0	0	1

Exercícios

1. Tabela Verdade para Operação OU
   Construa a tabela verdade para a expressão Booleana A + B + C + D. Liste todas as combinações possíveis das variáveis de entrada e determine o resultado da operação.

2. Tabela Verdade para Operação E
   Dada a expressão X × Y × Z, crie a tabela verdade correspondente. Certifique-se de listar todas as combinações possíveis das variáveis de entrada e calcule o resultado da operação.

3. Complementação de Variáveis
   Considere as variáveis Booleanas A e B. Determine os valores de saída para as expressões complementadas ¬A e ¬B. Em seguida, construa a tabela verdade para a expressão ¬A + ¬B.

4. Avaliação de Expressões Booleanas
   Avalie a expressão W = (A × B) + ¬C e construa a tabela verdade correspondente. Certifique-se de seguir a ordem de precedência das operações e inclua colunas intermediárias para as subexpressões.

5. Propriedades Associativa e Comutativa
   Verifique as propriedades associativa e comutativa para a operação OU utilizando as expressões (A + B) + C e (B + C) + A. Construa a tabela verdade e compare os resultados para confirmar as propriedades.

Entrega

icon: pen-to-square
date: 2025-04-22 10:20:00.00 -3
category:

• aula
• exercicio
  order: 4

---

Portas Lógicas

Já vimos que uma função Booleana pode ser representada por uma equação matemática ou detalhada por meio de sua tabela verdade. No entanto, além dessas formas, existe uma representação gráfica muito utilizada, na qual cada operador lógico é associado a um símbolo específico. Essa representação gráfica facilita o entendimento e a análise dos circuitos, pois permite o reconhecimento visual imediato das operações realizadas. Esses símbolos são conhecidos como portas lógicas.

Na prática, as portas lógicas não são apenas símbolos em um diagrama: elas correspondem a dispositivos eletrônicos reais, implementados por circuitos eletrônicos capazes de executar operações lógicas. Na eletrônica digital, que trabalha apenas com dois estados possíveis (0 e 1), o nível lógico 0 geralmente está associado à ausência de tensão elétrica (0 volt), enquanto o nível lógico 1 corresponde à presença de tensão (normalmente 5 volts, mas pode variar conforme a tecnologia). Portanto, ao estudarmos portas lógicas, estamos lidando tanto com a representação simbólica das operações da álgebra Booleana quanto com os componentes físicos que as realizam.

Nesta disciplina, focaremos no aspecto lógico das portas, mas é importante lembrar que, em sistemas digitais reais, essas portas são implementadas fisicamente em circuitos integrados. Assim, quando desenhamos um circuito lógico, estamos representando graficamente como as variáveis de entrada são processadas por diferentes portas para produzir uma saída, de acordo com uma determinada função Booleana. O conjunto de portas lógicas e suas conexões, que implementa uma equação Booleana, é chamado de circuito lógico.

Porta OU

A porta lógica OR (OU) realiza a operação lógica de adição (soma lógica). Seu símbolo é mostrado abaixo. Assim como na porta AND, as entradas são posicionadas à esquerda e a saída à direita. Uma porta OR pode ter duas ou mais entradas, mas sempre possui uma única saída. A saída será 1 se pelo menos uma das entradas for 1; caso contrário, será 0. O funcionamento da porta OR segue a definição da operação OU, detalhada em Álgebra Booleana e Circuitos Lógicos.

Símbolo da porta lógica OR com 2 entradas e com 3 entradas.

A tabela verdade da porta OR mostra que a saída será 1 sempre que pelo menos uma das entradas for 1. Isso significa que a porta OR é utilizada em situações onde se deseja detectar a presença de pelo menos um sinal ativo entre várias possibilidades.

Funcionamento da porta OU com o sinal variando com o tempo

Porta AND

A porta lógica AND (E) realiza a operação de multiplicação lógica. Seu símbolo é mostrado abaixo, com as entradas à esquerda (mínimo duas) e a saída única à direita. As linhas que representam as entradas e saídas podem ser vistas como fios que transportam sinais elétricos. A saída da porta AND será 1 somente se todas as entradas forem 1; caso contrário, será 0. O funcionamento da porta AND segue a definição da operação E, apresentada em Álgebra Booleana e Circuitos Lógicos.

Símbolo da porta lógica AND com 2 entradas e com 3 entradas.

A porta AND é fundamental em circuitos onde é necessário que todas as condições sejam satisfeitas para que a saída seja ativada, funcionando como um elemento de decisão.

Funcionamento da porta E com o sinal variando com o tempo

Inversor (ou Porta Inversora, ou Negador)

A porta lógica que realiza a operação de complementação é chamada de inversor (ou porta inversora, ou negador). Ela possui apenas uma entrada e uma saída. Sua função é inverter o valor lógico da entrada: se a entrada for 1, a saída será 0; se a entrada for 0, a saída será 1. Caso seja necessário inverter uma expressão mais complexa, primeiro calcula-se o resultado da expressão e, em seguida, aplica-se o inversor. O símbolo do inversor é mostrado abaixo:

Símbolo do inversor (também conhecido como negador ou porta inversora)

O inversor é essencial para criar funções lógicas mais complexas, permitindo a obtenção do valor oposto de uma variável ou expressão.

Porta NAND

A porta NAND (Not AND) realiza a operação inversa da porta AND. Ou seja, sua saída é igual à negação do resultado da operação AND entre as entradas. A saída da porta NAND será 0 apenas quando todas as entradas forem 1; em todos os outros casos, a saída será 1. O símbolo da porta NAND é semelhante ao da porta AND, mas possui um pequeno círculo na saída, indicando a negação.

Símbolo da porta lógica NAND com 2 entradas e com 3 entradas.

A porta NAND é muito utilizada na eletrônica digital, pois qualquer circuito lógico pode ser implementado apenas com portas NAND, devido à sua propriedade de universalidade.

Funcionamento da porta NAND com o sinal variando com o tempo

Porta NOR

A porta NOR (Not OR) realiza a operação inversa da porta OR. Sua saída é igual à negação do resultado da operação OR entre as entradas. Assim, a saída da porta NOR será 1 apenas quando todas as entradas forem 0; nos demais casos, a saída será 0. O símbolo da porta NOR é semelhante ao da porta OR, mas com um pequeno círculo na saída.

Símbolo da porta lógica NOR com 2 entradas e com 3 entradas.

Assim como a porta NAND, a porta NOR também é universal, podendo ser usada para construir qualquer circuito lógico.

Funcionamento da porta NOR com o sinal variando com o tempo

Circuito Lógico

Dada uma equação Booleana qualquer, é possível desenhar o circuito lógico correspondente, que implementa essa função. O circuito lógico é composto pelas portas lógicas necessárias para realizar as operações indicadas na equação, conectadas de acordo com a ordem das operações. As variáveis de entrada são representadas por linhas (fios) que conduzem os sinais, e as portas são conectadas para processar essas variáveis conforme a expressão.

Por exemplo, considere um sistema de controle industrial, onde sensores de temperatura e pressão monitoram um processo químico. Os sinais desses sensores são comparados com valores de referência, e se qualquer um dos parâmetros ultrapassar o limite, um alarme é acionado. O circuito lógico desse sistema pode ser representado como segue:

Circuito lógico para um sistema de controle de uma planta industrial

Para desenhar um circuito lógico a partir de uma equação Booleana, siga estes passos:

1. Identifique as variáveis de entrada: Cada variável é representada por uma linha horizontal.
2. Analise a expressão: Determine a ordem das operações, considerando a precedência dos operadores.
3. Desenhe as portas lógicas: Para cada operação (AND, OR, NOT, etc.), desenhe a porta correspondente e conecte as entradas e saídas conforme a expressão.
4. Conecte as portas: Siga a ordem das operações, conectando as saídas intermediárias às entradas das próximas portas, até obter a saída final.

Veja um exemplo para a expressão $W=X+Y\cdot \bar{Z}$:

Circuito lógico para a equação W = X + Y . ~Z

Expressões Booleanas

Na avaliação de expressões Booleanas, a ordem de precedência dos operadores é fundamental para garantir o resultado correto. A precedência é a seguinte:

1. Complementação (Negação): Avaliada primeiro.
2. Multiplicação Lógica (E, AND, $\cdot$): Tem prioridade sobre a adição lógica.
3. Adição Lógica (OU, OR, $+$): Avaliada por último.
4. Parênteses: Expressões entre parênteses têm precedência máxima.

Portanto, ao analisar uma expressão, resolva primeiro as operações dentro dos parênteses, depois as negações, em seguida as multiplicações lógicas e, por fim, as adições lógicas.

Circuitos lógicos são implementações físicas de expressões Booleanas. Todo circuito lógico é formado pela interligação de portas lógicas. A partir de um circuito lógico, é possível deduzir a expressão Booleana correspondente, e vice-versa. O domínio dessas relações é essencial para o projeto e análise de sistemas digitais.

Expressão executada pelo circuito

Para obter uma expressão Booleana a partir de um diagrama de circuito lógico, siga o caminho dos sinais das entradas até a saída, identificando as portas lógicas encontradas e aplicando os operadores correspondentes na ordem em que os sinais passam pelas portas.

Por exemplo:

• Expressão $A\cdot B+C$

  1. As entradas $A$ e $B$ passam por uma porta AND, resultando em $A\cdot B$.
  2. O resultado dessa porta AND e a entrada $C$ passam por uma porta OR, resultando em $A\cdot B+C$.

  

  Circuito lógico para A . B + C

• Expressão $(A+B)\cdot C$

  1. As entradas $A$ e $B$ passam por uma porta OR, resultando em $A+B$.
  2. O resultado dessa porta OR e a entrada $C$ passam por uma porta AND, resultando em $(A+B)\cdot C$.

  

  Circuito lógico para (A + B) . C

Assim, ao analisar o caminho dos sinais e as portas utilizadas, é possível escrever a expressão Booleana correspondente ao circuito.

Exercício

1. Obter as equações dos circuitos

   circuito

   

   equação

   1. As entradas $A$ e $B$ passam por uma porta OR, resultando em $A+B$.
   2. As entradas $C$ e $D$ passam por outra porta OR, resultando em $C+D$.
   3. As saídas dessas duas portas OR são conectadas a uma porta AND, resultando em $S=(A+B)\cdot (C+D)$.
   circuito

   

   equação

   1. As entradas $A$ e $B$ passam por uma porta AND, resultando em $A\cdot B$.
   2. A entrada $C$ passa por uma porta NOT, resultando em $\bar{C}$.
   3. As entradas $C$ e $D$ passam por uma porta NAND, resultando em $\overline{C\cdot D}$.
   4. As três saídas ($A\cdot B$, $\bar{C}$ e $\overline{C\cdot D}$) são conectadas a uma porta OR, resultando em $S=(A\cdot B)+\bar{C}+\overline{C\cdot D}$.
   circuito

   

   equação

   1. As entradas $A$ e $C$ passam por uma porta AND, resultando em $A\cdot C$.
   2. As entradas $A$ e $B$ passam por outra porta AND, resultando em $A\cdot B$.
   3. As saídas dessas duas portas AND são conectadas a uma porta OR, resultando em $(A\cdot C)+(A\cdot B)$.
   4. A entrada $C$ passa por uma porta NOT, resultando em $\bar{C}$.
   5. As entradas $B$ e $\bar{C}$ passam por uma porta AND, resultando em $B\cdot \bar{C}$.
   6. As saídas de $(A\cdot C)+(A\cdot B)$ e $B\cdot \bar{C}$ são conectadas a uma porta AND, resultando em $Y=[(A\cdot C)+(A\cdot B)]\cdot (B\cdot \bar{C})$.
   circuito

   

   equação

   1. A entrada $A$ passa por uma porta NOT, resultando em $\bar{A}$.
   2. As entradas $\bar{A}$, $B$ e $C$ passam por uma porta AND, resultando em $\bar{A}\cdot B\cdot C$.
   3. As entradas $A$ e $D$ passam por uma porta OR, resultando em $A+D$.
   4. A saída da porta OR passa por uma porta NOT, resultando em $\overline{A+D}$.
   5. As saídas $\bar{A}\cdot B\cdot C$ e $\overline{A+D}$ passam por uma porta AND, resultando em $S=(\bar{A}\cdot B\cdot C)\cdot \overline{A+D}$.
   circuito

   

   equação

   1. As entradas $A$ e $B$ passam por uma porta OR, resultando em $A+B$.
   2. O resultado de $A+B$ e a entrada $C$ passam por uma porta AND, resultando em $(A+B)\cdot C$.
   3. O resultado $(A+B)\cdot C$ passa por uma porta NOT, resultando em $\overline{(A+B)\cdot C}$.
   4. O resultado $\overline{(A+B)\cdot C}$ e a entrada $D$ passam por uma porta OR, resultando em $\overline{(A+B)\cdot C}+D$.
   5. O resultado $\overline{(A+B)\cdot C}+D$ e a entrada $E$ passam por uma porta AND, resultando em $S=(\overline{(A+B)\cdot C}+D)\cdot E$.

2. Determine o circuito definido por:

   • $X=A\cdot B\cdot C$
   • $X=A+\bar{B}$
   • $X=A\cdot C+B\cdot \bar{C}+\bar{A}\cdot B\cdot C$
   • $S=A\cdot B\cdot C+(A+B)\cdot C$

icon: pen-to-square
date: 2025-04-24 13:00:00.00 -3
category:

• aula
• exercicio
  order: 5

---

Derivação de Expressões Booleanas (Expressões booleana pela Tabela Verdade)

Podemos, ainda, obter expressões booleanas e circuitos lógicos a partir de tabelas verdade. Esse método é fundamental, pois, em muitos casos práticos, o comportamento desejado de um sistema digital é especificado diretamente por uma tabela verdade, que relaciona todas as possíveis combinações de entradas com as saídas correspondentes.

Há basicamente duas maneiras de se definir (ou descrever) uma função Booleana: descrevendo-se todas as situações das variáveis de entrada para as quais a função vale 1 ou, alternativamente, todas as situações em que a função vale 0. O primeiro método é conhecido por soma de produtos (SdP), enquanto que o segundo é chamado produto de somas (PdS). Qualquer função Booleana pode ser descrita por meio de soma de produtos ou por meio de produto de somas. Como as funções Booleanas só podem assumir um dentre dois valores (0 ou 1), basta usar-se um dos dois métodos para se encontrar uma equação para uma função

Soma de Produtos (SdP)

Dada uma função Booleana de $n$ variáveis (ou seja, $n$ entradas), haverá $2n$ combinações possíveis de valores. Dizemos que esse conjunto de valores que as variáveis podem assumir, juntamente com os respectivos valores da função, constituem o espaço da função. A cada combinação de entradas podemos associar um termo produto, no qual todas as variáveis da função estão presentes, e que é construído da seguinte forma: se a variável correspondente vale 0, ela deve aparecer negada; se a variável vale 1, ela deve aparecer não negada.

O procedimento consiste em analisar a tabela verdade e identificar todas as linhas em que a saída desejada é igual a 1 (verdadeira). Para cada uma dessas linhas, constrói-se um termo lógico (produto) que representa aquela combinação específica de entradas. Em seguida, todos esses termos são somados (adição lógica, OU) para formar a expressão booleana completa.

1. Liste todas as combinações de entrada: Monte a tabela verdade com todas as possíveis combinações das variáveis de entrada.
2. Identifique as linhas com saída 1: Observe em quais linhas a saída é igual a 1.
3. Monte um termo para cada linha: Para cada linha com saída 1, escreva um termo AND (produto) usando as variáveis de entrada. Se a variável for 1, use-a normalmente; se for 0, use seu complemento (negação).
4. Some todos os termos: A expressão booleana final será a soma (OR) de todos os termos obtidos.

Esse método é chamado de forma canônica de soma de produtos (SOP, do inglês Sum of Products).

Exemplo

Considere a seguinte tabela verdade para três variáveis ($A$, $B$, $C$):

A	B	C	S
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	1

As linhas em que $S=1$ são:

• (0, 0, 1): $\bar{A}\cdot \bar{B}\cdot C$
• (0, 1, 0): $\bar{A}\cdot B\cdot \bar{C}$
• (1, 0, 0): $A\cdot \bar{B}\cdot \bar{C}$
• (1, 1, 1): $A\cdot B\cdot C$

A expressão booleana será:

$$S=\bar{A}\cdot \bar{B}\cdot C+\bar{A}\cdot B\cdot \bar{C}+A\cdot \bar{B}\cdot \bar{C}+A\cdot B\cdot C$$

A fim de simplificar a notação, o símbolo da operação E pode ser omitido. Desta forma, a equação anterior pode ser reescrita de maneira mais concisa

$S=\overline{AB}C+\bar{A}B\bar{C}+A\overline{BC}+ABC$

Aplicação prática

Na prática, esse é o método mais comum para projetar circuitos lógicos a partir de requisitos funcionais, pois permite partir diretamente do comportamento desejado (tabela verdade) para a implementação física (circuito lógico). Após obter a expressão, pode-se simplificá-la usando as leis da álgebra Booleana, tornando o circuito mais eficiente.

Exercício

1. Obtenha a expressão que executa a tabela verdade a seguir e desenhe o circuito lógico

A	B	S
0	0	0
0	1	1
1	0	1
1	1	0

Produto de Somas (PdS)

O método de produto de somas (PdS) é uma alternativa ao soma de produtos para descrever funções booleanas a partir da tabela verdade. Nesse método, a expressão booleana é formada identificando todas as linhas em que a saída desejada é igual a 0 (falsa).

O procedimento consiste em:

1. Liste todas as combinações de entrada: Monte a tabela verdade com todas as possíveis combinações das variáveis de entrada.
2. Identifique as linhas com saída 0: Observe em quais linhas a saída é igual a 0.
3. Monte um termo para cada linha: Para cada linha com saída 0, escreva um termo OR (soma) usando as variáveis de entrada. Se a variável for 0, use-a normalmente; se for 1, use seu complemento (negação).
4. Multiplique todos os termos: A expressão booleana final será o produto (AND) de todos os termos obtidos.

Esse método é chamado de forma canônica de produto de somas (POS, do inglês Product of Sums).

Exemplo

Considere a seguinte tabela verdade para três variáveis ($A$, $B$, $C$):

A	B	C	S
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	1

As linhas em que $S=0$ são:

• (0, 0, 0): $A+B+C$
• (0, 1, 1): $A+\bar{B}+\bar{C}$
• (1, 0, 1): $\bar{A}+B+\bar{C}$
• (1, 1, 0): $\bar{A}+\bar{B}+C$

A expressão booleana será:

$$S=(A+B+C)\cdot (A+\bar{B}+\bar{C})\cdot (\bar{A}+B+\bar{C})\cdot (\bar{A}+\bar{B}+C)$$

Note que a ordem de precedência de uma expressão em produto de somas é “primeiro cada soma deve ser avaliada, para só então avaliar-se o produto”. Isto significa que os parêntesis em torno de cada termo soma são obrigatórios! Repare também que os símbolos referentes à operação E (entre os termos soma) podem ser omitido

$S=(A+B+C)(A+\bar{B}+\bar{C})(\bar{A}+B+\bar{C})(\bar{A}+\bar{B}+C)$

Aplicação prática

O método PdS é útil em situações onde é mais fácil identificar as condições em que a saída deve ser 0. Assim como no método SdP, a expressão obtida pode ser simplificada usando as leis da álgebra Booleana para otimizar o circuito lógico.

Exercício

1. Obtenha a expressão que executa a tabela verdade a seguir e desenhe o circuito lógico

A	B	S
0	0	1
0	1	0
1	0	0
1	1	1

Ou exclusivo

A porta lógica OU exclusivo (XOR, do inglês exclusive OR) realiza uma operação lógica especial: sua saída é 1 se, e somente se, o número de entradas em nível lógico 1 for ímpar (no caso de duas entradas, se as entradas forem diferentes). Para duas entradas $A$ e $B$, a saída $S$ é 1 apenas quando $A\ne B$.

O símbolo da porta XOR é semelhante ao da porta OR, mas com uma linha adicional na entrada.

Símbolo da porta lógica XOR (OU exclusivo) com 2 entradas.

A tabela verdade da porta XOR para duas entradas é:

A	B	$S=A\oplus B$
0	0	0
0	1	1
1	0	1
1	1	0

A expressão booleana para a porta XOR de duas entradas é:

$$S=(A\cdot \bar{B})+(\bar{A}\cdot B)$$

A porta XOR é muito utilizada em circuitos de soma, comparadores e sistemas onde é necessário detectar diferenças entre sinais.

Funcionamento da porta XOR com o sinal variando com o tempo

Implementação detalhada da porta XOR (OU exclusivo) usando portas AND, OR e NOT.

Não OU exclusivo

A porta lógica NÃO OU exclusivo (XNOR, do inglês exclusive NOR) realiza a operação inversa da porta XOR. Sua saída é 1 se, e somente se, o número de entradas em nível lógico 1 for par (no caso de duas entradas, se as entradas forem iguais). Para duas entradas $A$ e $B$, a saída $S$ é 1 apenas quando $A=B$.

O símbolo da porta XNOR é semelhante ao da porta XOR, mas com um pequeno círculo na saída, indicando a negação.

Símbolo da porta lógica XNOR (NÃO OU exclusivo) com 2 entradas.

A tabela verdade da porta XNOR para duas entradas é:

A	B	$S=A\odot B$
0	0	1
0	1	0
1	0	0
1	1	1

A expressão booleana para a porta XNOR de duas entradas é:

$$S=(A\cdot B)+(\bar{A}\cdot \bar{B})$$

A porta XNOR é utilizada em comparadores de igualdade e circuitos onde é necessário detectar se dois sinais são iguais.

Funcionamento da porta XNOR com o sinal variando com o tempo

Implementação detalhada da porta XNOR (NÃO OU exclusivo) usando portas AND, OR e NOT.

Leis Fundamentais e Propriedades da Álgebra Booleana

A álgebra Booleana é regida por um conjunto de leis e propriedades que definem o comportamento das variáveis e operações lógicas. Essas leis são fundamentais para simplificar expressões e projetar circuitos eficientes.

Sejam $A$ e $B$ duas variáveis Booleanas. O espaço Booleano é definido por:

Info

se $A\ne 0$, então $A=1$

se $A\ne 1$, então $A=0$

As operações elementares são: OU (adição lógica), E (multiplicação lógica) e complementação (negação). As principais propriedades são:

• Adição lógica (OU):

  $$\begin{array}{r}A+0=A\\ A+1=1\\ A+A=A\\ A+\bar{A}=1\end{array}$$

• Multiplicação lógica (E):

  $$\begin{array}{r}A\cdot 0=0\\ A\cdot 1=A\\ A\cdot A=A\\ A\cdot \bar{A}=0\end{array}$$

• Complementação:

  $$\begin{array}{r}\overline{\stackrel{―}{A}}=A\end{array}$$

• Comutatividade:

  $$\begin{array}{r}A+B=B+A\\ A\cdot B=B\cdot A\end{array}$$

• Associatividade:

  $$\begin{array}{r}A+(B+C)=(A+B)+C=(A+C)+B\\ A\cdot (B\cdot C)=(A\cdot B)\cdot C=(A\cdot C)\cdot B\end{array}$$

• Distributiva:

  $$\begin{array}{r}A\cdot (B+C)=A\cdot B+A\cdot C\end{array}$$

Essas leis permitem manipular e simplificar expressões Booleanas, facilitando o projeto de circuitos lógicos mais simples e eficientes.

Simplificação da expressão

Aplicando as propriedades de associatividade e distributiva da álgebra Booleana, é possível simplificar a equação acima. Por exemplo, ao agrupar e reorganizar os termos, podemos identificar fatores comuns e reduzir a expressão, tornando-a mais eficiente para implementação em circuitos lógicos. O uso dessas propriedades é fundamental para minimizar o número de portas lógicas necessárias e otimizar o projeto.

Vamos simplificar a expressão:

$$S=\bar{A}\cdot \bar{B}\cdot C+\bar{A}\cdot B\cdot \bar{C}+A\cdot \bar{B}\cdot \bar{C}+A\cdot B\cdot C$$

Agrupando termos semelhantes e aplicando as propriedades da álgebra Booleana, temos:

1. Observe que os termos podem ser agrupados em pares que diferem apenas por uma variável negada:

   • $\bar{A}\cdot \bar{B}\cdot C$ e $A\cdot B\cdot C$ (ambos têm $C$)
   • $\bar{A}\cdot B\cdot \bar{C}$ e $A\cdot \bar{B}\cdot \bar{C}$ (ambos têm $\bar{C}$)

2. Fatorando $C$ e $\bar{C}$:

   $$S=C\cdot (\bar{A}\cdot \bar{B}+A\cdot B)+\bar{C}\cdot (\bar{A}\cdot B+A\cdot \bar{B})$$

3. Note que:

   • $\bar{A}\cdot \bar{B}+A\cdot B=(A\odot B)$ (XNOR)
   • $\bar{A}\cdot B+A\cdot \bar{B}=(A\oplus B)$ (XOR)

4. Portanto, a expressão simplificada é:

   $$S=(A\odot B)\cdot C+(A\oplus B)\cdot \bar{C}$$

Ou seja, a saída $S$ é igual a XNOR de $A$ e $B$ quando $C=1$, ou XOR de $A$ e $B$ quando $C=0$.

Circuitos Combinacionais

Circuitos combinacionais são sistemas digitais nos quais as saídas, em qualquer instante, dependem apenas do estado atual das entradas. Diferentemente dos circuitos sequenciais, não há elementos de memória: não importa o histórico dos sinais, apenas o valor presente das entradas determina o valor das saídas.

Um circuito combinacional é composto por portas lógicas interligadas de modo a realizar uma função lógica específica. As principais características são:

• Sem memória: Não armazena estados anteriores.
• Saída instantânea: A saída depende apenas das entradas atuais.
• Função Booleana: Cada circuito pode ser descrito por uma expressão algébrica Booleana.

Exemplos clássicos: somadores, comparadores, multiplexadores, decodificadores, codificadores.

Estrutura Geral de um Circuito Combinacional

Todo circuito combinacional pode ser representado genericamente como um bloco com $n$ entradas e $m$ saídas, conforme o diagrama abaixo:

O diagrama acima mostra um circuito combinacional genérico, com três entradas ($E_1$, $E_2$, $E_3$) e duas saídas ($S_1$, $S_2$). O número de entradas e saídas pode variar conforme a aplicação.

Projeto de Circuitos Combinacionais

O projeto de circuitos combinacionais segue etapas bem definidas:

1. Especificação do problema: Definir claramente o que o circuito deve fazer.
2. Tabela verdade: Listar todas as combinações possíveis das entradas e as respectivas saídas desejadas.
3. Expressão Booleana: Derivar as funções lógicas para cada saída.
4. Simplificação: Simplificar as expressões usando álgebra Booleana ou mapas de Karnaugh.
5. Implementação: Montar o circuito usando portas lógicas básicas.

---

Exemplo Prático

Desenvolver um sistema automático para controlar os semáforos 1 e 2 presentes no cruzamento da RUA A e B. O sistema deve atender as seguintes características:

• Quando houver carros apenas na Rua B, o semáforo 2 deve permanecer verde.
• Quando houver carros apenas na Rua A, o semáforo 1 deve permanecer verde.
• Quando houver carros em ambas as Ruas, o semáforo para Rua A deve ser aberto.

Ilustração Cruzamento

Tabela Verdade

Considere as entradas:

• $A$: Carro na Rua A (1 = sim, 0 = não)
• $B$: Carro na Rua B (1 = sim, 0 = não)

As saídas:

• $S_1$: Semáforo 1 verde (Rua A)
• $S_2$: Semáforo 2 verde (Rua B)

$A$	$B$	$S_1$	$S_2$
0	0	0	0
0	1	0	1
1	0	1	0
1	1	1	0

Equações Booleanas

• $S_1=(A\cdot \bar{B})+(A\cdot B)$
  • $S_1=A(\bar{B}+B)$
  • $S_1=A\cdot 1$
  • $S_1=A$
• $S_2=\bar{A}\cdot B$

Circuito para controlar semáforo

Tensão, Corrente e Resistência

^[3]

Introdução

O estudo da robótica e o desenvolvimento de projetos exigem que saibamos como os componentes eletrônicos e os artefatos elétricos funcionam. Por isso, é extremamente importante compreendermos alguns conceitos básicos da Física, tais como tensão, corrente e resistência. Nesta aula, iremos revisar cada uma dessas grandezas. Vamos lá?

Ao elaborarmos projetos em robótica, é importante saber sobre a tensão a ser aplicada no circuito, bem como qual corrente elétrica deverá passar por este circuito. Do contrário, poderá ocorrer uma sobrecarga no circuito elétrico, danificando os componentes utilizados.

A eletrônica é o ramo da física e da engenharia que estuda e utiliza o comportamento dos elétrons em materiais, principalmente em semicondutores e condutores, para criar, controlar e manipular sinais elétricos. Ao controlar o movimento dos elétrons, é possível desenvolver circuitos capazes de realizar funções como amplificação, processamento, armazenamento e transmissão de informações. Esse controle é feito por meio de componentes eletrônicos, como resistores, capacitores, transistores e diodos, que direcionam, limitam ou modificam o fluxo da corrente elétrica conforme a necessidade do circuito. Assim, a eletrônica está presente em praticamente todos os dispositivos modernos, desde simples controles remotos até computadores e robôs complexos, permitindo o funcionamento eficiente e seguro desses sistemas.

Eletrônica

Eletrônica é o controle de movimento dos elétrons, controle da corrente elétrica.

Circuito

Circuito = Fonte + Condutores + Carga

Vamos iniciar compreendendo o que é uma corrente elétrica?

A corrente elétrica corresponde ao fluxo ordenado das partículas que possuem carga elétrica (elétrons ou íons) no interior de materiais diversos. Na figura abaixo, visualizamos a representação de um átomo. Em seu núcleo, há os prótons com cargas positivas e nêutrons com carga neutra; ao redor, na eletrosfera, os elétrons com carga negativa.

Representação de um átomo

Os elétrons, nas coisas, estão em movimento, porém de modo aleatório ou desordenado, conforme ilustrado na figura abaixo.

Movimento desordenado de elétrons livres

A corrente elétrica é gerada quando os elétrons se movimentam de modo ordenado, seguindo o mesmo fluxo, devido a uma diferença de potencial elétrico aplicada sobre eles. Tal fenômeno é o que faz artefatos, aparelhos e dispositivos eletrônicos funcionarem.

Os elétrons precisam de um meio material condutor para se movimentarem, o qual possibilita também, ao ser conectado a uma fonte de tensão, como a bateria representada na figura abaixo, o fluxo ordenado da carga negativa.

Movimento ordenado de elétrons em um condutor conectado a uma fonte de tensão

Materiais como alumínio, ouro, potássio, mercúrio e gases ionizados são condutores, e, na eletrônica, um exemplo clássico de condutor, muito utilizado em projetos e com baixa resistência elétrica, é o fio (ou cabo) de cobre.

Fios paralelo de cobre

Imagine que você está correndo ao redor da escola. Ao correr alguns metros, há elementos que podem se colocar "contra" o seu movimento: a direção do vento, a aderência de seu tênis ao solo, o conforto térmico, o controle da respiração, dentre outros. No caso da eletricidade, quando um elétron se movimenta, ele sofre uma força contrária em seu caminho, que é a resistência elétrica (veremos, na sequência, um pouco mais sobre o tema). Isto está relacionado, por exemplo, à espessura do fio ou cabo utilizado (sua dimensão poderá definir maior ou menor resistência elétrica) ou mesmo ao material que estiver em contato com a corrente elétrica, como a cerâmica ou o plástico, que são materiais isolantes e dificultam a movimentação dos elétrons.

Tensão

A tensão é a força que coloca os elétrons em movimento, ou seja, a força que cria a corrente elétrica.

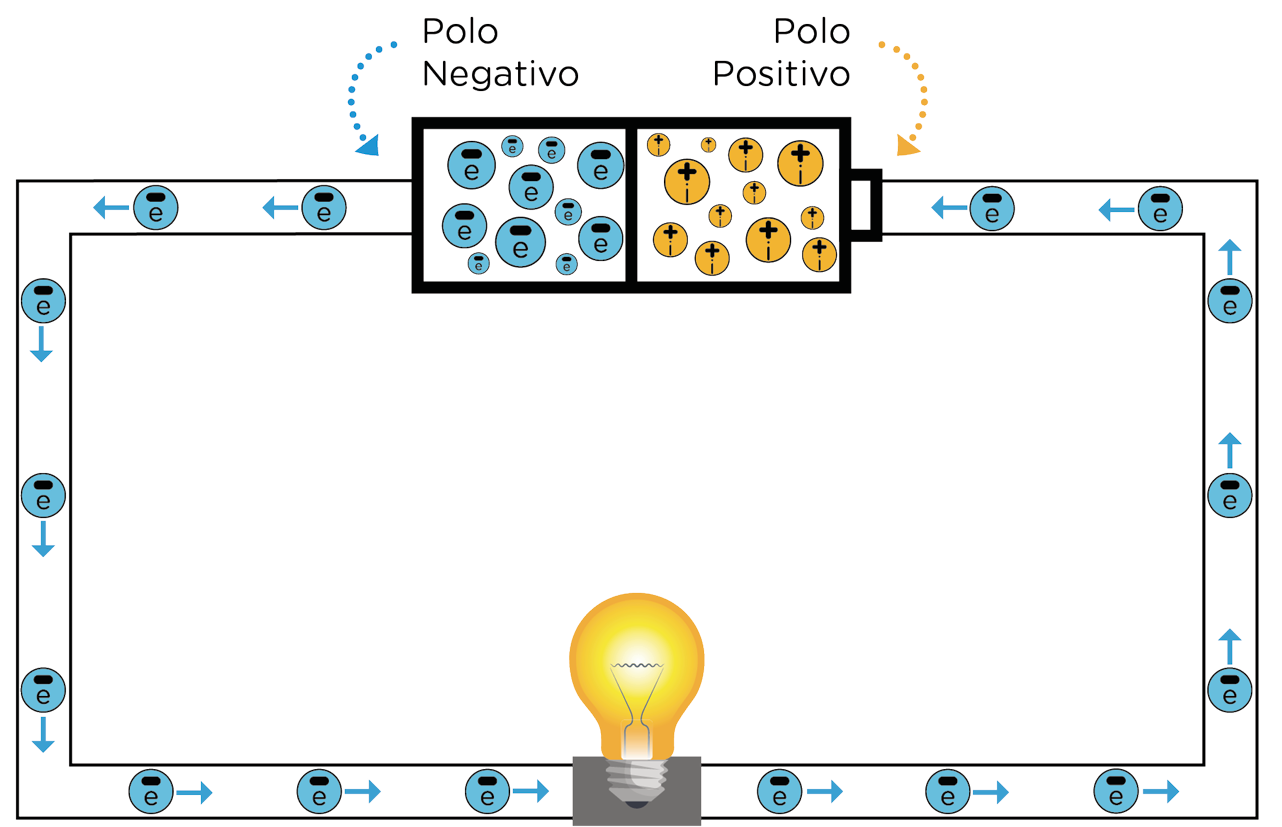
Como vimos, nos condutores a corrente elétrica é gerada pela movimentação ordenada dos elétrons. Por possuírem cargas de sinal negativo, tendem a seguir em direção ao maior potencial, que é o polo positivo. Esse é o sentido real da corrente elétrica - fluxo de elétrons do polo negativo para o polo positivo.

Na análise de circuitos elétricos, adota-se o sentido convencional, em que se atribui à carga dos elétrons o sinal positivo, o que resulta no movimento dos elétrons ao menor potencial, que é o polo negativo - fluxo de elétrons do polo positivo para o polo negativo.

A figura abaixo representa cada sentido ao ilustrar o processo de acendimento de uma lâmpada incandescente a partir de uma bateria.

Sentidos da corrente elétrica

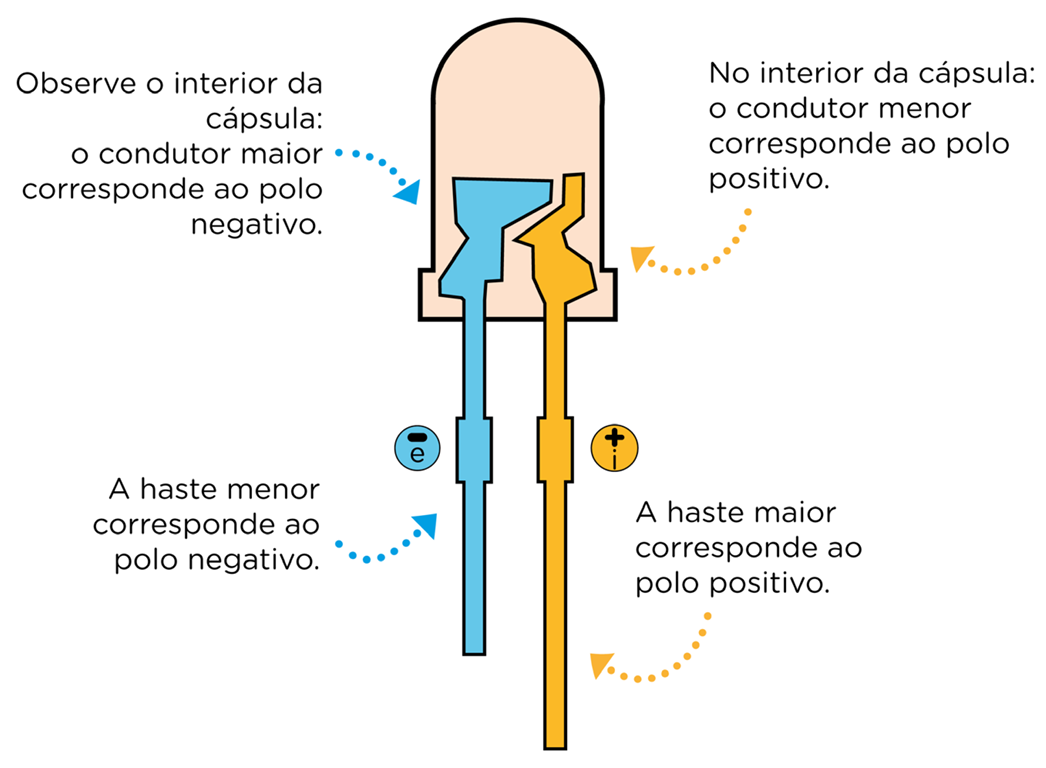
Que tal verificar, de modo prático, o funcionamento de um circuito e compreender o sentido da corrente quando ligamos um LED a uma bateria, tal como ilustrado na figura 5?

Para isso, observe a bateria 3V e o LED, veja que ambos possuem lados distintos, os quais correspondem aos polos positivo e negativo, conforme ilustrado a seguir:

Localização das polaridades do LED

Localização das polaridades da Bateria

Localizadas as polaridades, chegou o momento de conectar o LED à bateria, respeitando as polaridades no momento do encaixe.

Para esta atividade de funcionamento de um circuito, você pode utilizar também o simulador online Tinkercad.

Ao entrar no Tinkercad utilizando sua conta, localize no item “Componentes Básicos” o LED e a bateria 3V, arrastando-os até a área central de prototipagem. Então, clique sobre um dos pinos do LED, identificando sua polaridade, e siga com o cursor até a polaridade correspondente da bateria 3V. Repita o mesmo processo com a polaridade contrária, fechando o circuito, e clique no botão “Iniciar simulação”.

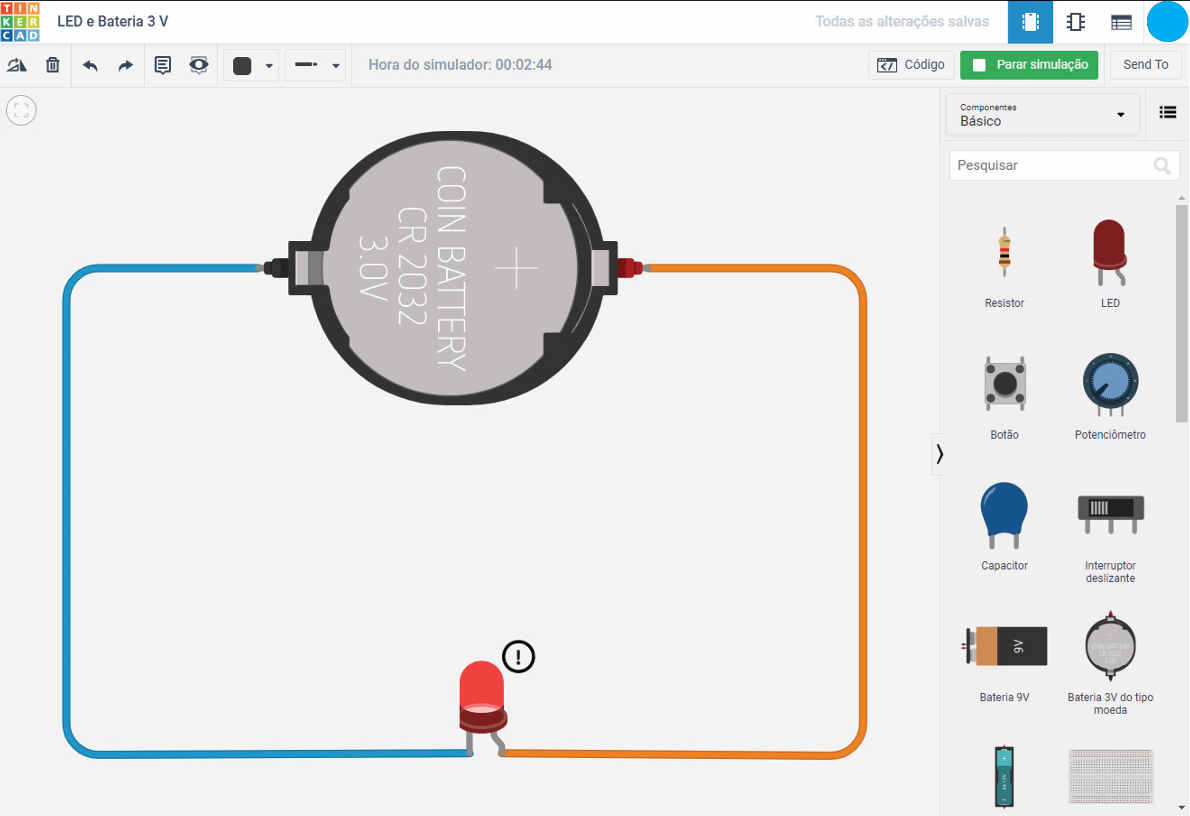
Fonte: Tinkercad

Nos experimentos acima, você verificou a polaridade e o sentido da corrente. Além disso, a corrente elétrica pode ter dois tipos de fluxo: fluxo ordenado ou com variações, o que caracteriza, respectivamente, as correntes Contínua (CC) e Alternada (CA), conforme o infográfico a seguir:

Corrente Contínua e Corrente Alternada

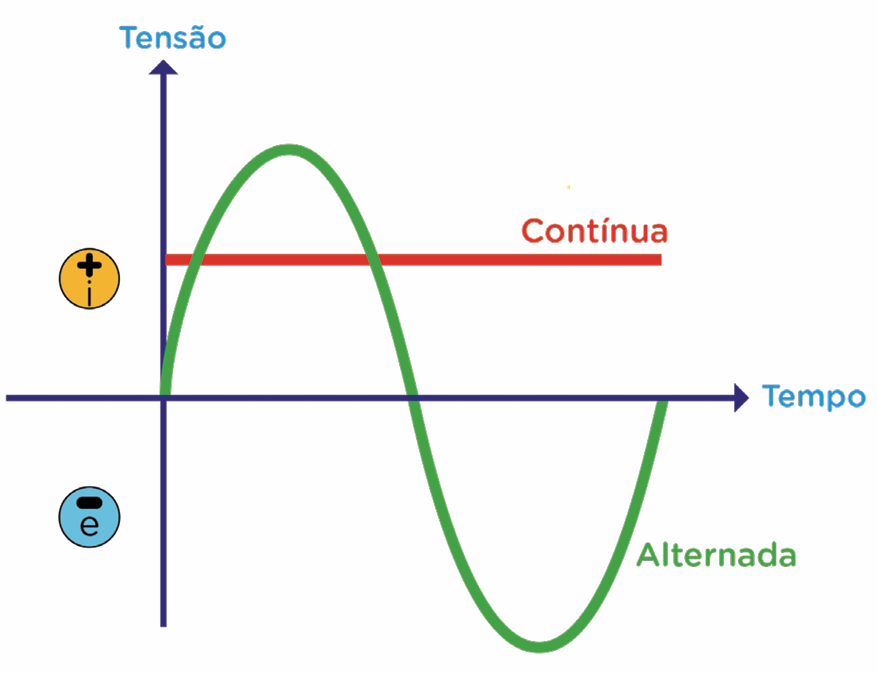
Corrente Contínua e Corrente Alternada

Corrente Contínua

O fluxo ordenado dos elétrons ocorre em apenas uma direção (positiva ou negativa), sem variação.

A corrente contínua é a mais comum em circuitos eletrônicos, como os utilizados em computadores, celulares e outros dispositivos. A bateria de 9V, fonte de celular, pilhas e placas solares são exemplos de fontes de corrente contínua.

Corrente Alternada

Fluxo dos elétrons com variação no decorrer do tempo e alternância entre tensão positiva e tensão negativa.

A quantidade de ciclos, em um determinado intervalo de tempo, é chamada de frequência. No caso de uma frequência de 60Hz, tem-se 60 ciclos por segundo.

A corrente alternada é a mais comum em circuitos elétricos, como os utilizados em residências e indústrias. A energia elétrica que chega às casas e empresas é um exemplo de corrente alternada, pois a tensão elétrica varia entre valores positivos e negativos.

Tensões de 120V, 127V, 220V e 240V são exemplos de tensões alternadas, que variam entre -170V e +170V. A corrente alternada é utilizada em eletrodomésticos, como geladeiras, micro-ondas e ar-condicionado.

A Batalha das Correntes | Trailer Oficial (2min49)

De grande relevância histórica e variados aspectos técnicos, o filme “A Batalha das Correntes” (“The Current War”, EUA, 2017), dirigido por Alfonso Gomez-Rejon, apresenta a disputa, ocorrida no final do século XIX, entre Thomas Edison (Benedict Cumberbatch), que já havia lançado a lâmpada incandescente, e George Westinghouse (Michael Shannon) e Nikola Tesla (Nicholas Hoult) acerca do sistema de distribuição de energia elétrica nos Estados Unidos. Enquanto Edison defendia a utilização da corrente contínua, Westinghouse e Tesla defenderam a corrente alternada.

Tesla vs. Edison: A Disputada Guerra das Correntes | Artigo

Tensão Elétrica

A tensão elétrica é a grandeza física que representa a diferença de potencial elétrico entre dois pontos de um circuito, determinando a quantidade de energia a ser fornecida ao circuito, permitindo, assim, o funcionamento de um equipamento ou artefato elétrico.

A tensão elétrica é a força que impulsiona os elétrons a se moverem em um circuito, criando a corrente elétrica. Ela é medida em volts (V) e pode ser gerada por diferentes fontes, como baterias, pilhas, geradores e tomadas elétricas.

tensão

força - funcionamento

Como um primeiro exemplo de artefato elétrico, podemos pensar na lâmpada incandescente, pois a diferença de potencial elétrico nas extremidades de seu filamento determinará sua luminosidade (atualmente, é mais comum o uso de lâmpadas de LED por conta de sua eficiência energética para iluminação, pois a lâmpada incandescente gera mais calor que luz). Outro exemplo que temos são os fornos elétricos, pois os filamentos que assarão as comidas são aquecidos pela transição de elétrons em barras de metal que apresentam resistência a eles - e a resistência, como veremos mais à frente, gera calor!

Treine Mais!

Que tal um exercício “prático” de calor gerado pela resistência?

Esfregue a sua mão, uma contra a outra, e perceba que ela gera calor. Agora, pense que uma de suas mãos é o elétron e a outra o metal por onde ele percorre o caminho. Com o atrito de ambos, é gerado calor e, algumas vezes, luz também!

Por isso, vários componentes eletrônicos, para terem um funcionamento otimizado, necessitam de algo que os resfrie, como, no caso de computadores e micro-ondas, aberturas na parte lateral e/ou traseira.

No caso de baterias, uma das fontes de tensão que nos acompanhará ao longo de nossos projetos, a diferença de potencial elétrico entre os polos determinará sua força elétrica. O tempo de duração da bateria dependerá da quantidade de carga presente nela.

Exemplo de fonte de tensão elétrica

De acordo com o Sistema Internacional de Unidades, a unidade de medida volt (V) é a unidade da tensão elétrica ou da diferença de potencial elétrico (ddp) que representa o potencial de transmissão de energia. No caso de uma bateria de 9V, um dos itens que pode compor variados projetos de robótica, por exemplo, a diferença de potencial elétrico entre seus polos positivo e negativo é de 9V, o que convencionou, então, a referência à bateria como “bateria 9V”.

A diferença de potencial é importante porque a corrente elétrica só se dará nos momentos em que houver diferença de potencial elétrico.

Na montagem de projetos em robótica, a regulagem da tensão e da corrente aplicada, por exemplo, na montagem do circuito de um robô, são importantes. Caso não haja um controle ou aplicação correta da corrente elétrica no projeto, poderão ocorrer danos nos componentes utilizados.

Resistência Elétrica

Resistência elétrica é uma grandeza que indica o quanto um determinado condutor se opõe à passagem da corrente elétrica, dificultando o fluxo de elétrons.

Os componentes presentes em um artefato eletrônico, tais como Resistores, Capacitores e Fusíveis, compõem o circuito elétrico pelo qual a corrente elétrica passará e em todo este caminho haverá uma resistência. Com o movimento de elétrons livres no condutor, conforme suas características, pode haver uma maior colisão entre estes elétrons, o que acarretaria em uma limitação da quantidade de elétrons presentes na corrente elétrica.

Leis de Ohm

A eletricidade lida com variadas grandezas e equações. Dentre as equações, destacamos a Primeira Lei de Ohm, formulada pelo físico e matemático Georg Simon Ohm (1789 – 1854) a partir de experimentos com a variação de tensão em um circuito e a percepção, em cálculos, de que há uma proporcionalidade entre a diferença de potencial e a corrente elétrica, além de uma razão constante entre as três principais grandezas: corrente elétrica (cuja unidade é Ampère - A), tensão elétrica ou diferença de potencial elétrico (cuja unidade é Volt - V) e resistência elétrica (cuja unidade é Ohm - Ω). Partindo da Primeira Lei de Ohm, é possível calcular a tensão e a corrente presente em qualquer ponto de circuitos eletrônicos.

Mas afinal, o que nos informa esta Lei de Ohm?

Na Primeira Lei de Ohm temos que a resistência elétrica em um condutor é equivalente à razão da diferença de potencial entre seus terminais pela corrente que flui pelo condutor. Assim, é possível determinar qual corrente perpassará um circuito com a aplicação de determinada tensão entre seus terminais, estabelecendo, assim, as especificações de um projeto.

Por se tratar de uma razão constante entre as grandezas, a Primeira Lei de Ohm pode ser calculada através das seguintes equações:

Equações Primeira Lei de Ohm

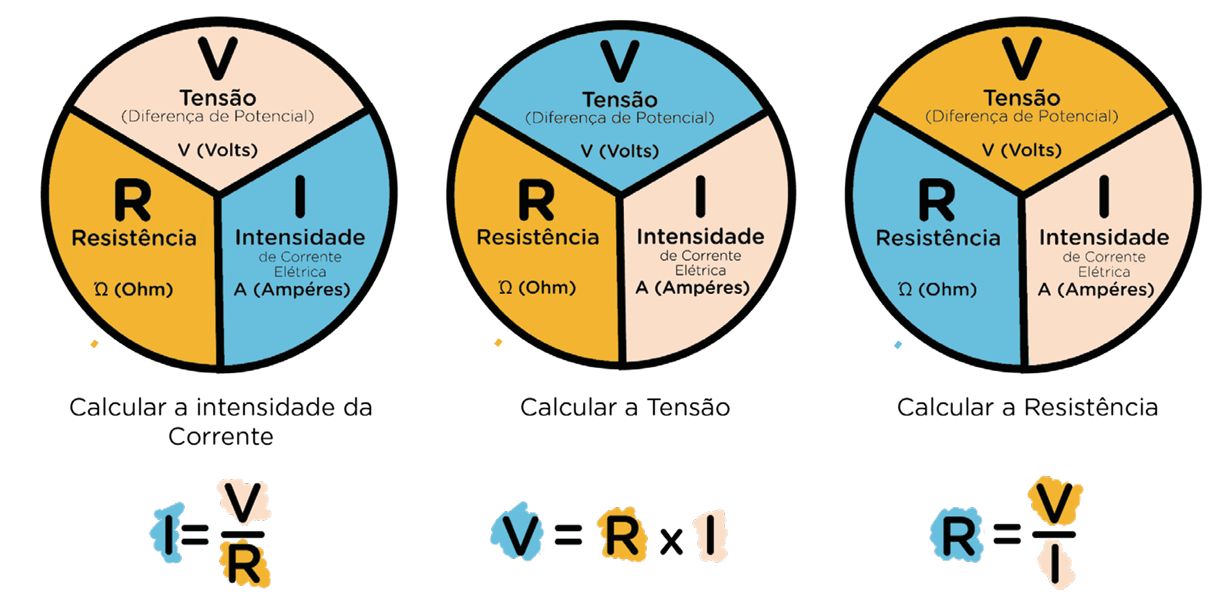
Onde:

• V = Tensão elétrica ou ddp (V)
• R = Resistência elétrica (Ω)
• I = Intensidade da corrente elétrica (A)

Treine Mais!

A plataforma de prototipagem Tinkercad possui um espaço de aprendizagem. Na lição Ohm’s Law, tutorial composto por cinco etapas e disponível em inglês, você poderá aprender sobre um conceito fundamental em design de circuito, a Lei de Ohm, e o aplicará para garantir o acendimento de um LED com segurança.

Bateria 9V conectada a um LED

Fonte: Tinkercad

Como a eletricidade se trata do movimento de elétrons, a eletrônica, também aliada à robótica, tem a ver com isso, com o que a gente usa para controlar este movimento dos elétrons: se irão para um lado ou para o outro, se serão transformados em luz, som, calor etc.

Tente agora com uma bateria 9V

Referências

Arduino

Introdução ao Arduino

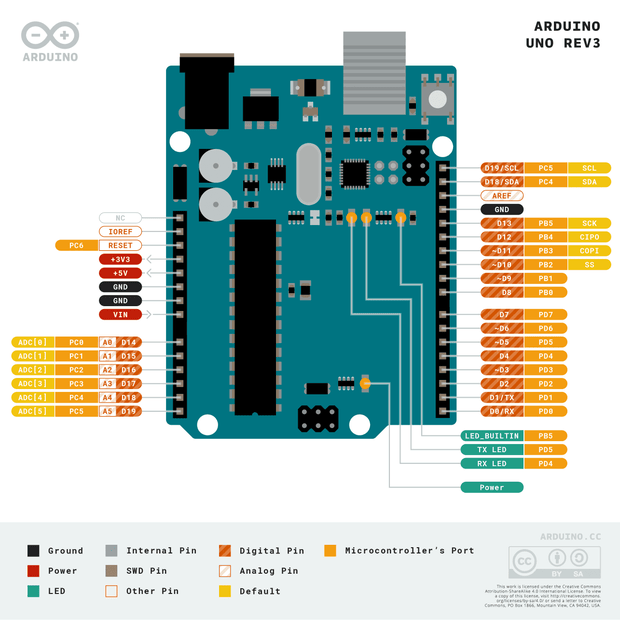
O Arduino é uma plataforma de prototipagem eletrônica de código aberto baseada em hardware e software de fácil utilização. Foi criada em 2005 por um grupo de pesquisadores do Instituto de Design de Interação de Ivrea, na Itália, com o objetivo de facilitar o aprendizado de eletrônica e programação.

Componentes Básicos

Hardware

• Placa Arduino (UNO, Nano, Mega, etc.)
• Microcontrolador ATmega
• Portas digitais e analógicas
• Conexão USB
• Regulador de tensão
• LEDs indicadores

Software

• IDE Arduino
• Linguagem de programação baseada em C/C++
• Bibliotecas extensivas
• Monitor serial

Estrutura Básica de um Programa

void setup() {
  // Configurações iniciais
  // Executado uma vez
}

void loop() {
  // Código principal
  // Executado continuamente
}

Funções Fundamentais

Entradas e Saídas Digitais

• pinMode()
• digitalWrite()
• digitalRead()

Entradas Analógicas

• analogRead()
• analogWrite()

Projetos Práticos

1. LED Piscante

O primeiro projeto básico para iniciantes:

void setup() {
  pinMode(13, OUTPUT);
}

void loop() {
  digitalWrite(13, HIGH);
  delay(1000);
  digitalWrite(13, LOW);
  delay(1000);
}

2. Sensor de Luz

Utilizando LDR para medição de luminosidade:

void setup() {
  Serial.begin(9600);
}

void loop() {
  int valorLuz = analogRead(A0);
  Serial.println(valorLuz);
  delay(100);
}

Comunicação Serial

A comunicação serial é fundamental para:

• Depuração de código
• Monitoramento de sensores
• Interação com computador
• Comunicação entre dispositivos

Boas Práticas

1. Comentar o código adequadamente
2. Utilizar nomes descritivos para variáveis
3. Organizar o código em funções
4. Fazer backup dos projetos
5. Verificar conexões antes de energizar

Recursos Adicionais

• Site oficial Arduino

Arduino e Tinkercad

Turma no Tinkercad

Add a heading

Arduino e Tinkercad são duas ferramentas poderosas que estão ganhando popularidade no mundo da eletrônica e da engenharia. Embora ambas as ferramentas sejam comumente usadas por amadores e profissionais, muitas pessoas podem não ter ouvido falar delas ou podem não entender completamente o que são.

O que é Tinkercad?

Tinkercad é uma plataforma online que permite aos usuários projetar e simular modelos 3D. É uma ferramenta gratuita e fácil de usar que é projetada para iniciantes e especialistas. Com o Tinkercad, os usuários podem criar modelos 3D de objetos, edifícios e muito mais, e depois exportá-los para impressão 3D ou uso em outros projetos. Tinkercad também tem uma variedade de recursos que o tornam ideal para uso educacional, como planos de aula, tutoriais e ideias de projetos.

Arduino e Tinkercad Juntos

Uma das coisas mais interessantes sobre Arduino e Tinkercad é que eles podem ser usados juntos. O Tinkercad possui uma gama de componentes eletrônicos que podem ser usados para construir circuitos e dispositivos de controle, e também possui um simulador Arduino integrado que permite aos usuários programar e testar seus circuitos em um ambiente virtual. Isso facilita o protótipo e o teste de novas ideias antes de construí-las no mundo real.

No geral, Arduino e Tinkercad são duas ferramentas poderosas que estão transformando o mundo da eletrônica e da engenharia. Seja você um amante, artista, designer ou educador, essas ferramentas oferecem infinitas possibilidades de criação e inovação.

Circuito Elétrico

^[3:1]

Circuito Elétrico: Conceitos e Componentes

Um circuito elétrico é um caminho fechado por onde a corrente elétrica pode circular, permitindo o funcionamento de dispositivos eletrônicos e elétricos. Para compreender como montar e analisar circuitos, é fundamental conhecer seus principais conceitos e componentes.

Componentes Básicos de um Circuito Elétrico

Um circuito elétrico é composto por diversos componentes, cada um com uma função específica. Abaixo estão os principais componentes encontrados em circuitos elétricos:

1. Fonte de Energia

A fonte de energia é o componente responsável por fornecer a diferença de potencial (tensão) necessária para que os elétrons se movimentem pelo circuito. Exemplos comuns incluem:

• Pilhas e baterias: Fornecem energia química convertida em energia elétrica. Possuem polos positivo (+) e negativo (–).
• Fontes de alimentação: Dispositivos que convertem a energia da rede elétrica em tensão adequada para o circuito.

Exemplo de Fonte de Alimentação

O diagrama acima mostra uma fonte de alimentação conectada a uma lâmpada, representando um circuito simples. A fonte fornece a tensão necessária para o funcionamento do circuito.

2. Condutores

Os condutores são materiais que permitem a passagem da corrente elétrica com facilidade. Nos circuitos, geralmente utilizamos fios de cobre revestidos por material isolante. Eles conectam todos os componentes, formando o caminho por onde os elétrons circulam.

Exemplo de Condutor

O exemplo acima mostra um fio condutor simples, representando a ligação entre dois pontos do circuito.

3. Resistores

Os resistores são componentes que limitam o fluxo de corrente elétrica, convertendo parte da energia elétrica em calor. Eles são essenciais para proteger outros componentes e controlar a intensidade da corrente. Os valores dos resistores são medidos em ohms (Ω) e identificados por códigos de cores.

Exemplo de Resistor

O diagrama acima mostra um resistor conectado entre dois pontos do circuito.

4. Interruptores (Chaves)

Interruptores são dispositivos que abrem ou fecham o circuito, controlando o fluxo de corrente. Quando o interruptor está aberto, o circuito é interrompido e a corrente não circula. Quando está fechado, o circuito é completado e a corrente pode fluir.

Exemplo de Interruptor

O diagrama acima mostra um interruptor (chave) em um circuito.

5. Cargas

A carga é o componente que consome energia elétrica para realizar algum trabalho, como:

• Lâmpadas: Convertem energia elétrica em luz e calor.
• Motores: Transformam energia elétrica em movimento.
• Dispositivos eletrônicos: Como sensores, microcontroladores, etc.

Exemplo de Lâmpada

O diagrama acima mostra uma lâmpada como carga no circuito.

6. Dispositivos de Proteção

São componentes que protegem o circuito contra sobrecargas e curtos-circuitos, como:

• Fusíveis: Se a corrente ultrapassar um valor seguro, o fusível se rompe, interrompendo o circuito.
• Disjuntores: Funcionam como interruptores automáticos, desligando o circuito em caso de falha.

Exemplo de Fusível

O diagrama acima mostra um fusível conectado ao circuito.

7. Placa de Protoboard

A protoboard é uma placa utilizada para montar circuitos temporários sem a necessidade de solda. Ela possui furos conectados internamente, facilitando a conexão dos componentes e a realização de testes.

Exemplo de Protoboard (Representação Simples)

O diagrama acima representa uma protoboard de forma simplificada.

8. Esquema de Montagem

Um circuito elétrico pode ser representado por um diagrama esquemático, onde cada componente é simbolizado de forma padronizada. Isso facilita a compreensão, montagem e manutenção do circuito.

Exemplo de Esquema de Montagem

O diagrama acima mostra um esquema de montagem simples com bateria, resistor e lâmpada.

Exemplo de Circuito Simples

Um circuito básico pode ser composto por uma bateria, um resistor, uma lâmpada e um interruptor, todos conectados por fios condutores. Ao fechar o interruptor, a corrente flui da bateria, passa pelo resistor (limitando a corrente), acende a lâmpada e retorna à bateria, completando o ciclo.

Referências

Programação em Blocos no Tinkercad

^[4]

A programação em blocos no Tinkercad oferece uma maneira intuitiva de criar programas para controlar seus circuitos eletrônicos. Utilizando uma interface gráfica, você pode arrastar e soltar blocos de código para construir a lógica do seu projeto sem a necessidade de escrever código manualmente.

Para exemplificar, iremos projetar um semáforo no Tinkercad.

Como fazer um semáforo no Tinkercad?

O circuito que iremos utilizar está ilustrado na imagem abaixo:

Circuito do Semáforo no Tinkercad

• Conecte o LED verde (pedestres) à porta digital 12 do Arduino.
• Conecte o LED vermelho (pedestres) à porta digital 11 do Arduino.
• Conecte o LED verde (veículos) à porta digital 10 do Arduino.
• Conecte o LED amarelo (veículos) à porta digital 9 do Arduino.
• Conecte o LED vermelho (veículos) à porta digital 8 do Arduino.
• Certifique-se de que os componentes estão corretamente aterrados e alimentados, usando um resistor de 330Ω entre o terminal positivo dos LEDs e os pinos digitais do Arduino.
• Vá para a aba de “Código” e selecione “Blocos + Texto” como modo de edição. Você verá uma área de trabalho onde poderá arrastar blocos de código.

A ligação dos LEDs do semáforo com o Arduino ficará assim:

Tabela

Funcionamento do semáforo no Tinkercad

O sistema coordenado de semáforos para pedestre e veículos é essencial para garantir a segurança de todos no trânsito, prevenindo acidentes e organizando o fluxo de veículos e pedestres de maneira eficiente. O sistema funciona da seguinte forma:

Semáforo veículos e pedestres

• Quando o semáforo para veículos estiver verde, o semáforo para pedestres estará vermelho.
• Quando o semáforo para veículos mudar de verde para amarelo, o semáforo para pedestre ainda estará vermelho.
• Quando o semáforo para veículos estiver vermelho, o semáforo de pedestre estará verde.
• Um pouco antes do semáforo para veículos mudar de vermelho para verde, o semáforo para pedestres irá piscar a lâmpada vermelha.

Depois disso, o ciclo recomeça. Portanto, Teremos 4 fases:

Fases

Essa divisão por fases irá ajudar a configurar os blocos para o funcionamento do semáforo no Tinkercad.

Programa em blocos para semáforo

Para criar o código em blocos do semáforo no Tinkercad, dividiremos a lógica em 4 fases, como indicado na tabela acima:

A primeira delas é acender o LED verde dos veículos e o LED vermelho dos pedestres. Todos os outros LEDs devem estar desligados.

Referências

Push Button: Fundamentos, Funcionamento e Aplicações

Introdução

O push button (botão de pressão) é um dos componentes mais simples e importantes da eletrônica. Ele permite ao usuário interagir com circuitos, enviando comandos de ligar ou desligar, iniciar ou parar processos, ou alterar estados de dispositivos. Seu uso é fundamental em sistemas embarcados, automação, robótica, interfaces homem-máquina e projetos educacionais.

O que é um Push Button?

Um push button é um interruptor momentâneo: ele fecha o contato elétrico apenas enquanto está pressionado. Quando solto, o circuito é aberto novamente. Existem diversos tipos de push button, mas todos funcionam segundo o mesmo princípio: permitir ou interromper o fluxo de corrente elétrica.

Estrutura Física

O push button é composto por dois pares de terminais. Ao pressionar o botão, os contatos internos se unem, permitindo a passagem de corrente. Quando o botão é liberado, os contatos se separam, interrompendo o circuito.

Símbolo em Diagramas

O símbolo do push button em diagramas elétricos é representado por uma chave momentânea:

Funcionamento Elétrico

Quando o push button é inserido em um circuito, ele pode ser usado para:

• Fechar um circuito e permitir que a corrente flua (ligar um LED, motor, etc.)
• Enviar um sinal de entrada para um microcontrolador (como o Arduino)

Ligações Comuns

1. Em série com carga: O botão controla diretamente o fluxo de corrente para o dispositivo (ex: LED).
2. Como entrada digital: O botão é ligado a um pino de entrada do microcontrolador, que detecta seu estado e executa ações programadas.

Conceitos Fundamentais

Corrente, Tensão e Resistência

• Corrente elétrica: Fluxo de elétrons que percorre o circuito quando o botão está pressionado.
• Tensão: Diferença de potencial entre os terminais do botão, que impulsiona a corrente.
• Resistência: Utilizada para limitar a corrente e proteger componentes como LEDs.

Resistor Pull-down

Quando usamos push button como entrada digital em microcontroladores, é necessário garantir que o pino de entrada não fique "flutuando" (sem valor definido) quando o botão não está pressionado. O resistor pull-down conecta o pino ao GND, garantindo nível LOW (0V) quando o botão está aberto.

Aplicações do Push Button

• Controle de dispositivos (LEDs, motores, relés)
• Interfaces de usuário (painéis, teclados, controles)
• Sistemas de senha e autenticação
• Contadores e cronômetros
• Jogos eletrônicos
• Robótica educacional

Exemplos de Uso

1. Controle direto de carga

O push button pode ser usado para ligar/desligar um LED, motor ou outro dispositivo, simplesmente fechando o circuito.

2. Controle digital via microcontrolador

O botão envia um sinal para o microcontrolador, que interpreta o comando e executa ações programadas (acender LED, iniciar motor, etc.).

Cuidados ao Utilizar Push Button

• Sempre utilize resistores para limitar corrente em cargas como LEDs.
• Use resistor pull-down ou pull-up para garantir leituras estáveis em entradas digitais.
• Verifique a polaridade dos componentes (LEDs, microcontroladores).

Exercício Prático: Controle de LED com Push Button (Duas Abordagens)

Após estudar os conceitos, realize o exercício abaixo para fixar o conteúdo:

Controle de LED com Push Button: Duas Abordagens

Materiais Necessários

• 1 placa Arduino (Uno, Nano, etc.)
• 2 LEDs
• 2 resistores de 220Ω (um para cada LED)
• 2 push buttons
• 2 resistores de 10kΩ (pull-down para os botões)
• Jumpers
• Protoboard

Tarefa 1: Push Button Interrompendo Energia do LED (Circuito Simples)

Monte um circuito em que o push button é ligado em série com o LED e o resistor. Quando o botão está pressionado, a corrente passa e o LED acende. Quando o botão é solto, o circuito é interrompido e o LED apaga. Nesse caso, o push button controla diretamente o fluxo de corrente para o LED e o arduino é utilizado somente para alimentar o circuito.

Montagem:

• LED1 em série com resistor de 220Ω e push button1.
• Conecte tudo entre o VCC (5V) e o GND da protoboard.

Funcionamento:

O LED1 acende apenas enquanto o botão1 estiver pressionado, pois o botão fecha o circuito.

Exemplo de Circuito Simples com Push Button

Circuito simples com push button controlando LED

O diagrama acima mostra um circuito simples: a bateria fornece energia, o resistor limita a corrente, o push button controla o fluxo e o LED acende quando o botão é pressionado.

Tarefa 2: Push Button Controlando LED via Arduino

Monte um circuito em que o push button envia sinal para o Arduino, que então liga ou desliga o LED conforme o botão é pressionado.

Montagem:

• LED2 conectado ao pino digital 13 do Arduino, com resistor de 220Ω.
• Push button2 conectado ao pino digital 2 do Arduino, com resistor de 10kΩ (pull-down).
• Arduino alimentado via USB.

Funcionamento:
Quando o botão2 é pressionado, o Arduino detecta o sinal HIGH e acende o LED2. Quando o botão é solto, o LED2 apaga.

Resumo das Diferenças

• Tarefa 1: O botão controla diretamente o LED, sem lógica ou programação.
• Tarefa 2: O botão envia sinal ao Arduino, que decide quando ligar o LED via código.

Aplicações Práticas

Esses circuitos são a base para diversos projetos, como:

• Controle de dispositivos por botões
• Sistemas de senha
• Contadores
• Jogos eletrônicos
• Interruptores inteligentes

Entrega

Sensor de Distância: Fundamentos, Funcionamento e Aplicações

Introdução

O sensor de distância é um componente essencial em muitos sistemas eletrônicos, permitindo medir a distância entre o sensor e um objeto. Ele é amplamente utilizado em robótica, automação industrial, veículos autônomos e dispositivos de segurança.

O que é um Sensor de Distância?

Um sensor de distância é um dispositivo que detecta a presença de objetos e mede a distância até eles. Existem vários tipos de sensores de distância, incluindo ultrassônicos, infravermelhos e a laser. Cada tipo utiliza princípios físicos diferentes para medir a distância.

Tipos Comuns de Sensores de Distância

• Sensor Ultrassônico: Emite ondas sonoras de alta frequência e mede o tempo que leva para o eco retornar após refletir em um objeto.
• Sensor Infravermelho: Emite luz infravermelha e mede a intensidade da luz refletida para calcular a distância.
• Sensor a Laser: Emite um feixe de laser e mede o tempo que leva para o feixe refletido retornar ao sensor.
• Sensor de Efeito Hall: Mede a distância com base na variação do campo magnético.

Estrutura Física

Um sensor de distância geralmente consiste em um emissor (que pode ser um transdutor ultrassônico, LED infravermelho ou laser) e um receptor (microfone, fotodetector ou fototransistor). O emissor envia um sinal, e o receptor capta o sinal refletido de um objeto próximo.

Exemplo de uso

Nesse projeto o sensor de distância é utilizado para medir a distância entre o sensor e um objeto, como uma parede ou um obstáculo. O sensor envia um sinal ultrassônico e calcula a distância com base no tempo que leva para o eco retornar.

// C++ code
//
int distancia = 0;

int limiteVerde = 0;

int limiteAmarelo = 0;

long readUltrasonicDistance(int triggerPin, int echoPin)
{
  pinMode(triggerPin, OUTPUT);  // Clear the trigger
  digitalWrite(triggerPin, LOW);
  delayMicroseconds(2);
  // Sets the trigger pin to HIGH state for 10 microseconds
  digitalWrite(triggerPin, HIGH);
  delayMicroseconds(10);
  digitalWrite(triggerPin, LOW);
  pinMode(echoPin, INPUT);
  // Reads the echo pin, and returns the sound wave travel time in microseconds
  return pulseIn(echoPin, HIGH);
}

void setup()
{
  pinMode(LED_BUILTIN, OUTPUT);
  pinMode(13, OUTPUT);
  pinMode(12, OUTPUT);
  pinMode(11, OUTPUT);
  Serial.begin(9600);

  limiteVerde = 180;
  limiteAmarelo = 100;
  digitalWrite(LED_BUILTIN, LOW);
  digitalWrite(13, LOW);
  digitalWrite(12, LOW);
  digitalWrite(11, LOW);
}

void loop()
{
  Serial.println(distancia);
  distancia = 0.01723 * readUltrasonicDistance(2, 2);
  if (distancia >= limiteVerde) {
    // Ligar o Verde
    digitalWrite(11, HIGH);
    digitalWrite(12, LOW);
    digitalWrite(13, LOW);
  }
  if (distancia < limiteVerde) {
    // Ligar o Amarelo
    digitalWrite(11, HIGH);
    digitalWrite(12, LOW);
    digitalWrite(13, HIGH);
  }
  if (distancia < limiteAmarelo) {
    // Ligar o Vermelho
    digitalWrite(11, LOW);
    digitalWrite(12, LOW);
    digitalWrite(13, HIGH);
  }
  delay(10); // Delay a little bit to improve simulation performance
}

A cor do LED indica a distância medida pelo sensor:

• Verde: Distância maior que 180 cm.
• Amarelo: Distância entre 100 cm e 180 cm.
• Vermelho: Distância menor que 100 cm.

Ponte H: Fundamentos, Funcionamento e Aplicações

Introdução

A ponte H é um circuito eletrônico fundamental para controlar motores de corrente contínua (CC) e motores de passo. Ela permite inverter a direção do motor e controlar sua velocidade, sendo amplamente utilizada em robótica, automação e projetos de controle de movimento.

O que é uma Ponte H?

A ponte H é um arranjo de transistores ou relés que permite controlar a direção de rotação de um motor CC. O nome "ponte H" vem do arranjo dos componentes, que se assemelha à letra "H".

Estrutura Física

Uma ponte H típica consiste em quatro transistores (ou relés) dispostos em um formato de "H". Dois transistores controlam a corrente em uma direção, enquanto os outros dois controlam a corrente na direção oposta. Abaixo está um diagrama simplificado de uma ponte H:

Ponte H

Funcionamento

Para controlar a direção do motor, os transistores S1 e S4 são ativados para permitir a passagem de corrente em uma direção, enquanto S2 e S3 são desativados. Para inverter a direção, S2 e S3 são ativados, enquanto S1 e S4 são desativados. Isso permite que o motor gire em ambas as direções.

Ativação do motor

Inversão da Direção do Motor

Inversão do motor

Exemplo

Referências

• AULA 7 - Microcontroladores - IFSC
• Datasheet L298N, L293D

IC L293D e PWM

^[5]

Compreendendo os princípios básicos do controle motor

Antes de aprender sobre o driver do motor L293D, é importante entender dois conceitos principais:

• Circuito H-Bridge – permite controlar o sentido de rotação do motor
• PWM (modulação por largura de pulso) – ajuda a controlar a velocidade de um motor DC

Controlando a velocidade com PWM (modulação por largura de pulso)

Quando uma tensão fixa é aplicada a um motor CC, ele gira a uma velocidade fixa. Se você quiser alterar a velocidade, precisará ajustar a tensão. Uma tensão mais alta faz o motor girar mais rápido, enquanto uma tensão mais baixa o torna mais lento.

No entanto, alterar fisicamente a voltagem o tempo todo não é muito prático. É aí que entra a PWM, ou Modulação por Largura de Pulso.

PWM é uma maneira inteligente de controlar a quantidade média de potência enviada ao motor. Em vez de enviar uma tensão fixa, o PWM liga e desliga a tensão rapidamente em pulsos muito rápidos.

A “largura” de cada pulso ON, também chamado de ciclo de trabalho, determina por quanto tempo a tensão fica “ON” durante cada ciclo.

• Se a tensão estiver LIGADA na maior parte do tempo (um pulso mais amplo), o motor recebe uma tensão média mais alta e gira mais rápido.
• Se a tensão estiver desligada na maior parte do tempo (um pulso mais estreito), o motor receberá uma tensão média mais baixa e girará mais devagar.

A imagem abaixo mostra como diferentes ciclos de trabalho produzem diferentes tensões médias, que por sua vez afetam a velocidade do motor.

Técnica PWM de modulação por largura de pulso com ciclos de trabalho

CI driver de motor L293D

O L293D é um circuito integrado (CI) muito popular e amplamente utilizado, projetado principalmente para acionar cargas indutivas, como motores CC, motores de passo, relés e solenoides. Ele funciona como um amplificador de corrente, ou seja, recebe os sinais de controle de baixa corrente de um microcontrolador (como um Arduino) e os eleva para os níveis de corrente e tensão mais altos necessários para o funcionamento dos motores.
Circuito integrado L293D

Circuito integrado L293D

Potência do L293D

O L293D é bastante flexível em termos de potência. Ele pode operar com uma ampla faixa de tensões, de 4,5 V a 36 V, o que significa que é compatível com diversos tipos de motores.

Além disso, o L293D também é capaz de lidar com uma quantidade razoável de corrente. Cada canal do L293D pode fornecer até 600 miliamperes (mA) de corrente contínua e suportar picos curtos de até 1,2 amperes (A) por canal. Embora esses números possam parecer pequenos, eles são perfeitos para a maioria dos motores pequenos que amadores e estudantes costumam usar em seus projetos.

Pinagem do CI do driver do motor L293D

O L293D tem 16 pinos no total.
Pinagem do CI do driver do motor de ponte H dupla L293D

Pinagem do CI do driver do motor de ponte H dupla L293D

Vamos analisar cada grupo de pinos para entender o que eles fazem e como funcionam.

Pinos de energia

O L293D requer duas fontes de energia separadas:

Conexões de alimentação L293D

VSS (VCC1)alimenta o circuito lógico interno do CI. Você conectará este pino a uma fonte de alimentação de 5 V.

VS (VCC2)fornece energia aos motores. Você pode conectar qualquer tensão entre 4,5 V e 36 V, dependendo do motor utilizado.

GNDOs pinos são as conexões de aterramento comuns. O CI possui quatro pinos de aterramento, todos conectados internamente. Esses pinos têm duas funções importantes: fornecem um ponto de referência comum para todas as tensões no circuito e, igualmente importante, auxiliam na dissipação de calor.

Info

Motores são cargas indutivas e podem consumir correntes significativas, especialmente durante a partida, mudanças de direção ou sob carga pesada. Esse alto fluxo de corrente através dos transistores de ponte H internos gera calor. Esses múltiplos pinos de aterramento atuam como condutores térmicos, permitindo que o calor gerado dentro do CI seja conduzido para os trilhos de cobre na Placa de Circuito Impresso (PCB) à qual estão soldados. Ao conectar esses pinos a um grande vazamento de cobre ou plano de aterramento na PCB, a própria PCB atua como um dissipador de calor, ajudando a evitar que o CI superaqueça e entre em seu estado de desligamento térmico.

Pinos de saída do motor

Esses são os pinos onde você realmente conecta seus motores CC.

Terminais de saída L293D

Os pinos OUT1 e OUT2 conectam-se ao seu primeiro motor (motor A), enquanto os pinos OUT3 e OUT4 conectam-se ao seu segundo motor (motor B). Você pode conectar qualquer motor CC que funcione com 5 a 36 volts a esses pinos.

Pinos de controle de direção

Esses pinos controlam a direção de rotação dos motores ligando e desligando os interruptores internos da ponte H:

Entradas de controle de direção L293D

O chip possui dois pinos de controle de direção para cada motor. Os pinosIN1 e IN2 controlam a direção de rotação do motor A, enquanto os pinos IN3 e IN4 controlam a direção de rotação do motor B.

Ao definir diferentes combinações de sinais ALTO ou BAIXO nesses pinos, você pode fazer os motores girarem para frente, para trás ou parar. A table abaixo mostra exatamente como isso funciona:

Demonstração de controle de direção do motor L293D

IN1	IN2	Direção de rotação
Baixo(0)	Baixo(0)	Motor desligado
Alto(1)	Baixo(0)	Avançar
Baixo(0)	Alto(1)	Para trás
Alto(1)	Alto(1)	Motor desligado

Pinos de controle de velocidade

Os pinos ENAe ENB controlam a velocidade com que seus motores giram.

Entradas de controle de velocidade L293D

Na verdade, esses pinos funcionam como simples interruptores liga/desliga. Ao puxar um deles para a posição ALTA, o motor correspondente é ativado e gira em velocidade máxima com base nas suas entradas de direção. Ao puxá-lo para a posição BAIXA, o motor é completamente desativado e não gira.

Mas esses pinos podem fazer mais do que apenas ligar ou desligar os motores. Ao enviar um sinal PWM (Modulação por Largura de Pulso) para ENA ou ENB, você pode controlar a velocidade de cada motor.

Com o PWM, você habilita e desabilita o motor rapidamente, várias vezes por segundo. A chave é o ciclo de trabalho, ou seja, quanto tempo o sinal permanece LIGADO em cada ciclo. Um tempo LIGADO mais longo significa que o motor fica ativo por mais tempo do ciclo, então ele gira mais rápido. Um tempo LIGADO mais curto significa que ele fica habilitado por menos tempo por ciclo, então ele gira mais lentamente.

Exemplo

Referências

Conectando motores ao Arduino usando o L293D

^[5:1]

Agora é hora de conectar o driver do motor L293D a um Arduino e controlar alguns motores!

Começaremos conectando a energia aos motores. Neste experimento, estamos usando motores TT, comumente usados em robôs com tração em duas rodas. Esses motores geralmente funcionam bem com tensões entre 3 V e 6 V. Como usaremos uma fonte de alimentação externa de 5 V para nossos motores, precisamos conectar esses 5 V ao pino VS (VCC2) do L293D.

Em seguida, precisamos alimentar o circuito lógico dentro do L293D. Para isso, conectaremos o pino VSS (VCC1) ao pino de saída de 5 V do Arduino.

Além disso, é muito importante garantir que tudo compartilhe um aterramento comum; isso significa conectar um pino de aterramento do seu Arduino a uma conexão de aterramento na fonte de alimentação do seu motor externo e também conectar o pino GND do L293D ao aterramento do Arduino.

Uma vez feitas as conexões de energia, podemos conectar os pinos de controle. O L293D possui dois pinos de habilitação (ENA e ENB) e quatro pinos de entrada (IN1, IN2, IN3 e IN4). Conectaremos ENA ao pino 9 do Arduino, IN1 ao pino 8, IN2 ao pino 7, IN3 ao pino 5, IN4 ao pino 4 e ENB ao pino 3.

Tips

Vale a pena notar que os pinos 9 e 3 no Arduino são habilitados para PWM, o que significa que podemos usá-los mais tarde para controlar a velocidade dos motores usando PWM.

Por fim, conectaremos nossos motores. Pegue um motor e conecte seus dois fios aos pinos OUT1 e OUT2 do L293D. Em seguida, conecte o segundo motor aos pinos OUT3 e OUT4. Não se preocupe muito com qual fio vai para qual pino de saída do motor; você pode trocá-los se o motor girar na direção oposta à esperada, pois não existe uma maneira única "certa" ou "errada" de conectá-los.

Aqui está uma tabela de referência rápida para as conexões dos pinos:

Conexões do L293D com o Arduino

Pino L293D	Conexão Arduino
GND	GND
ENA	9
IN1	8
IN2	7
IN3	5
IN4	4
ENB	3

A imagem abaixo mostra o diagrama de fiação completo para esta configuração.

Conexão do CI do driver do motor L293D com motores DC Arduino

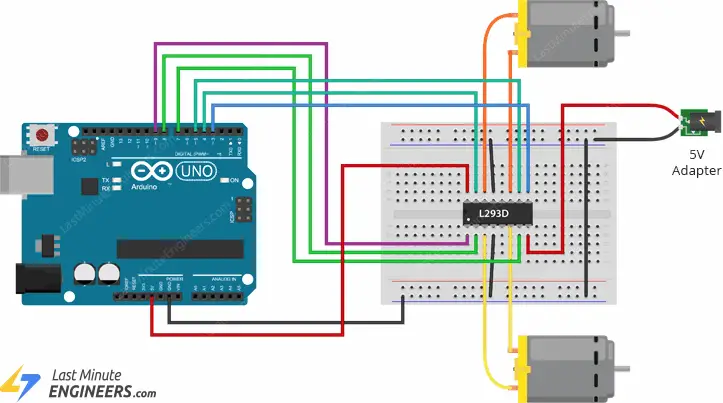
Código de exemplo do Arduino

Aqui está um esboço simples do Arduino que mostra como controlar a direção e a velocidade de dois motores CC usando o driver de motor L293D e um Arduino. Você não precisa de nenhuma biblioteca especial para este esboço; ele usa apenas as funções básicas integradas do IDE do Arduino.

Este exemplo é uma ótima maneira de adquirir experiência prática com o L293D para controlar a velocidade e a direção de motores. Depois de entender isso, você poderá construir facilmente sistemas de controle de motores mais complexos, como os usados em robôs básicos ou carros de controle remoto.

// Motor A connections
int enA = 9;
int in1 = 8;
int in2 = 7;
// Motor B connections
int enB = 3;
int in3 = 5;
int in4 = 4;

void setup() {
  // Set all the motor control pins to outputs
  pinMode(enA, OUTPUT);
  pinMode(enB, OUTPUT);
  pinMode(in1, OUTPUT);
  pinMode(in2, OUTPUT);
  pinMode(in3, OUTPUT);
  pinMode(in4, OUTPUT);

  // Turn off motors - Initial state
  digitalWrite(in1, LOW);
  digitalWrite(in2, LOW);
  digitalWrite(in3, LOW);
  digitalWrite(in4, LOW);
}

void loop() {
  directionControl();
  delay(1000);
  speedControl();
  delay(1000);
}

// This function lets you control spinning direction of motors
void directionControl() {
  // Set motors to maximum speed
  digitalWrite(enA, HIGH);
  digitalWrite(enB, HIGH);

  // Turn on motor A & B
  digitalWrite(in1, HIGH);
  digitalWrite(in2, LOW);
  digitalWrite(in3, HIGH);
  digitalWrite(in4, LOW);
  delay(2000);

  // Now change motor directions
  digitalWrite(in1, LOW);
  digitalWrite(in2, HIGH);
  digitalWrite(in3, LOW);
  digitalWrite(in4, HIGH);
  delay(2000);

  // Turn off motors
  digitalWrite(in1, LOW);
  digitalWrite(in2, LOW);
  digitalWrite(in3, LOW);
  digitalWrite(in4, LOW);
}

// This function lets you control speed of the motors
void speedControl() {
  // Turn on motors
  digitalWrite(in1, LOW);
  digitalWrite(in2, HIGH);
  digitalWrite(in3, LOW);
  digitalWrite(in4, HIGH);

  // Accelerate from zero to maximum speed
  for (int i = 0; i < 256; i++) {
    analogWrite(enA, i);
    analogWrite(enB, i);
    delay(20);
  }

  // Decelerate from maximum speed to zero
  for (int i = 255; i >= 0; --i) {
    analogWrite(enA, i);
    analogWrite(enB, i);
    delay(20);
  }

  // Now turn off motors
  digitalWrite(in1, LOW);
  digitalWrite(in2, LOW);
  digitalWrite(in3, LOW);
  digitalWrite(in4, LOW);
}

Info

Ao acelerar ou desacelerar um motor CC, você pode ouvir um zumbido, especialmente em valores de PWM mais baixos. Não se preocupe — isso é completamente normal. Isso acontece porque os motores CC precisam de uma certa quantidade mínima de tensão para começar a girar e, em valores de PWM baixos, a tensão pode não ser alta o suficiente para manter o motor funcionando sem problemas.

Explicação do código

No início do esboço, definimos quais pinos do Arduino serão usados para controlar o Motor A e o Motor B. Para o Motor A, temos um pino para habilitá-lo (permitindo-nos controlar sua velocidade com PWM) e dois pinos para controle de direção. Da mesma forma, para o Motor B, temos um pino de habilitação e dois pinos de controle de direção.

// Motor A connections
int enA = 9;
int in1 = 8;
int in2 = 7;

// Motor B connections
int enB = 3;
int in3 = 5;
int in4 = 4;

Na função setup(), configuramos todos os seis pinos de controle do motor como saídas, pois estamos enviando sinais do Arduino para o L293D. Também garantimos que ambos os motores estejam desligados, configurando todos os pinos de controle de direção para LOW. Isso garante que os motores não comecem a girar repentinamente quando o Arduino for ligado.

void setup() {
  // Set all the motor control pins to outputs
  pinMode(enA, OUTPUT);
  pinMode(enB, OUTPUT);
  pinMode(in1, OUTPUT);
  pinMode(in2, OUTPUT);
  pinMode(in3, OUTPUT);
  pinMode(in4, OUTPUT);

  // Turn off motors - Initial state
  digitalWrite(in1, LOW);
  digitalWrite(in2, LOW);
  digitalWrite(in3, LOW);
  digitalWrite(in4, LOW);
}

Na função loop(), chamamos duas funções personalizadas com um intervalo de um segundo entre elas. A primeira função é directionControl(), e a segunda é speedControl().

void loop() {
  directionControl();
  delay(1000);
  speedControl();
  delay(1000);
}

Vamos analisar o que cada uma dessas funções faz.

A função directionControl() demonstra como controlar a direção de ambos os motores. Primeiro, ajustamos ambos os motores à velocidade máxima possível, configurando ambos os pinos de habilitação em nível ALTO. Em seguida, enviamos os sinais necessários aos pinos de controle de direção para fazer com que os motores A e B girem para frente. Após girarem nessa direção por dois segundos, transferimos os sinais para seus pinos de direção, o que faz com que ambos os motores invertam a direção de rotação por mais dois segundos. Por fim, paramos os motores configurando todos os pinos de controle de direção em nível BAIXO.

void directionControl() {
  // Set motors to maximum speed
  digitalWrite(enA, HIGH);
  digitalWrite(enB, HIGH);

  // Turn on motor A & B
  digitalWrite(in1, HIGH);
  digitalWrite(in2, LOW);
  digitalWrite(in3, HIGH);
  digitalWrite(in4, LOW);
  delay(2000);

  // Now change motor directions
  digitalWrite(in1, LOW);
  digitalWrite(in2, HIGH);
  digitalWrite(in3, LOW);
  digitalWrite(in4, HIGH);
  delay(2000);

  // Turn off motors
  digitalWrite(in1, LOW);
  digitalWrite(in2, LOW);
  digitalWrite(in3, LOW);
  digitalWrite(in4, LOW);
}

A função speedControl() demonstra como controlar a velocidade dos motores usando PWM. Começamos configurando os pinos de controle de direção para que ambos os motores girem na mesma direção. Em seguida, aumentamos lentamente a velocidade do motor, elevando gradualmente o valor de PWM de 0 a 255. Isso simula um efeito de aceleração. Assim que os motores atingem a velocidade máxima, invertemos o processo — diminuindo lentamente o valor de PWM de 255 para 0, o que faz com que os motores diminuam gradualmente a velocidade e parem. Por fim, paramos os motores configurando todos os pinos de controle de direção para BAIXO.

void speedControl() {
  // Turn on motors
  digitalWrite(in1, LOW);
  digitalWrite(in2, HIGH);
  digitalWrite(in3, LOW);
  digitalWrite(in4, HIGH);

  // Accelerate from zero to maximum speed
  for (int i = 0; i < 256; i++) {
    analogWrite(enA, i);
    analogWrite(enB, i);
    delay(20);
  }

  // Decelerate from maximum speed to zero
  for (int i = 255; i >= 0; --i) {
    analogWrite(enA, i);
    analogWrite(enB, i);
    delay(20);
  }

  // Now turn off motors
  digitalWrite(in1, LOW);
  digitalWrite(in2, LOW);
  digitalWrite(in3, LOW);
  digitalWrite(in4, LOW);
}

Exemplo

Referências

---

1. STALLINGS, Williams. Arquitetura e Organização de Computadores. 10. ed. São Paulo: Pearson, 2017. ISBN: 9788543020532. ↩︎

2. Tanenbaum, Andrew S.; Austin, Todd. Organização Estruturada de Computadores. 6. ed. São Paulo: Pearson Education do Brasil, 2013. ISBN: 9788576059457. ↩︎

3. ESCOLA DIGITAL PR. Material didático. Disponível em: https://aluno.escoladigital.pr.gov.br/re-m1. ↩︎ ↩︎

4. Adaptado de: Como fazer um semáforo no Tinkercad: Programação em blocos - MakerHero ↩︎

5. https://lastminuteengineers.com/l293d-dc-motor-arduino-tutorial/ ↩︎ ↩︎